Nachdem wir den NFA nun eingeführt haben, macht es Sinn, dass wir uns als nächstes gleich die Frage stellen, in welchem Verhältnis er zum DFA steht? Kann der DFA mehr als der NFA? Kann der NFA mehr als der DFA? Können beide das gleiche? Sind sie unvergleichbar?
Mehr zu „können“ bezieht sich hierbei auf die akzeptierten Sprachen. Der NFA kann dann mehr als der DFA, wenn es zu jeder Sprache \(M\), zu der es einen DFA gibt, der \(M\) akzeptiert, auch einen NFA gibt, der \(M\) akzeptiert, und ferner, wenn es eine Sprache \(M‘\) gibt, für die zwar ein NFA konstruiert werden kann, aber kein DFA.
Was man recht schnell sehen kann, ist, dass jeder DFA auch als spezieller NFA angesehen werden kann, der NFA also mindestens all das kann, was der DFA kann. Seine spezielle Fähigkeit zu einem Buchstaben mehrere Kanten aus einem Zustand heraus zu haben, brauch der NFA ja gar nicht benutzen und ist dann im Grunde ein DFA. Will man dies formal ausführen, so sei \(\delta_D\) die Überführungsfunktion eines DFA und \(z_0\) sein Startzustand. Man setzt dann $$ \delta_N(z,x) := \{\delta_D(z,x)\} $$und $$ Z_{start} := \{z_0\} $$für die Überführungsfunktion \(\delta_N\) und die Startzustandsmenge \(Z_{start}\) des NFA. Zustandsmenge, Eingabealphabet und Endzustandsmenge übernimmt man für den NFA. Ist \(A\) der DFA und \(B\) der so konstruierte NFA, so kann man \(L(A) = L(B)\) sehr einfach zeigen, da im Grunde genau das gleiche passiert, nur das in der erweiterten Überführungsfunktion im ersten Argument einmal ein Zustand steht (beim DFA) und einmal eine einelementige Menge mit gerade diesem Zustand (beim NFA).
Die spannende Frage ist nun also, ob es auch andersherum geht, ob man also zu jedem NFA \(A\) einen DFA \(B\) konstruieren kann mit \(L(A) = L(B)\) oder ob es eine Sprache gibt, die ein NFA akzeptieren kann, aber kein DFA.
Wenn wir noch einmal die Arbeitsweise des NFA betrachten, dann stellen wir fest, dass der NFA stets (nichtdeterministisch) in einer Menge von Zuständen sein kann, also in einer Teilmenge seiner Zustandsmenge. Dies erkennt man auch gut an der erweiterten Überführungsfunktion, bei der im ersten Argument ja gerade diese Menge an Zuständen gesammelt wird.
Sei \(Z\) die Zustandsmenge des NFA, dann gibt es gerade \(2^{|Z|}\) viele Teilmengen von \(Z\). Dies sind zwar recht viele, aber es sind endlich viele! Erinnern wir uns an die Konstruktionsmethoden für DFAs, so könnte ein vielversprechender Ansatz also sein, sich in den Zuständen des DFAs gerade diese Teilmengen der Zustände des NFAs zu merken. Die Übergänge könnten dann gerade so gelingen, wie wir dies beim NFA machen, soll heißen: Wenn wir beim NFA \(\hat{\delta}(M,xw) = \hat{\delta}(M‘,w)\) haben, so wechseln wir im DFA aus dem Zustand, in dem wir uns gemerkt haben, dass der NFA nichtdeterministisch in den Zuständen aus \(M\) ist, nun in den Zustand, in dem wir uns dies für \(M‘\) merken. Genau dies passiert ja beim NFA. Vor dem Lesen von \(x\) ist er nichtdeterministisch in den Zuständen aus \(M\), danach nichtdeterministisch in den Zuständen aus \(M‘\). Diese Übergänge lassen sich dann also durch die Überführungsfunktion des NFA ermitteln.
Als Startzustand macht dann die Menge der Startzustände des NFA Sinn, denn in diesen Zuständen ist der NFA ja zu Anfang nichtdeterministisch. Bleibt die Endzustandsmenge zu definieren. Da wir im NFA dann akzeptieren, sobald in der Menge, in der der NFA sich nichtdeterministisch befindet, am Ende ein Endzustand ist, könne wir versuchen im DFA all jene Zustände zu Endzuständen zu machen, in denen wir uns eine Menge \(M\) merken, in der gerade ein Endzustand ist.
Mit diesen Überlegungen können wir zu jedem NFA einen DFA konstruieren und tatsächlich kann man beweisen, dass diese Konstruktion das Gewünschte leistet. Wir fassen die Konstruktion nun noch einmal formal zusammen, machen dann ein Beispiel und zeigen dann, dass die Konstruktion korrekt ist.
Satz 2.2.5
Zu jeder von einem NFA \(A\) akzeptierte Menge \(L\) kann ein DFA \(B\) konstruiert werden mit \(L(B) = L\).Beweis
Wir geben zunächst die oben bereits intuitiv beschriebene Konstruktion an. Sei dazu \(A = (Z, \Sigma, \delta, Z_{start}, Z_{end})\) ein NFA. Wir definieren einen DFA \(B = (Z‘, \Sigma‘, \delta‘, z_0, Z_{end}‘)\) wie folgt:- \(Z‘ := 2^Z\)
- \(\Sigma‘ := \Sigma\)
- \(\delta'(M,x) := \cup_{z \in M} \delta (z,x)\) oder alternativ
\(\delta'(M,x) := \cup_{z \in M} \{z‘ \in Z \mid (z,x,z‘) \in K\}\) - \(z_0 := Z_{start}\)
- \(Z_{end}‘ := \{M \in 2^Z \mid M \cap Z_{end} \not= \emptyset\}\)
Bevor wir beweisen, dass diese Konstruktion korrekt ist, dass also tatsächlich \(L(B) = L(A)\) gilt, führen wir die Konstruktion an einem Beispiel aus. Im Anschluss setzen wir den Beweis dann fort.
Betrachten wir die formale Konstruktion noch einmal. Die Menge der Zustände \(Z'\) des DFA ist gerade die Menge aller Teilmengen der Zustandsmenge \(Z\) des NFA. Ist also z.B. \(\{z_0, z_1\} \subseteq Z\), so ist diese Menge von Zuständen des NFA nun ein einzelner Zustand des DFA. Das Eingabealphabet wurde einfach übernommen, da ja weiterhin die gleichen Symbole gelesen werden sollen. Der Startzustand des DFA ist gerade die Menge der Startzustände des NFA (denn in einem dieser Zustände startet ja jede Rechnung des NFA) und die Endzustände des DFA sind all jene Mengen von Zuständen des NFA, die mindestens einen Endzustand des NFA enthalten (denn endet eine Rechnung des NFA in einem Endzustand, d.h. befindet sich in der Menge der Zustände, in denen er sich nichtdeterministisch nach Lesen eines Eingabewortes befindet, ein Endzustand, so akzeptiert er und dann soll auch der DFA akzeptieren). Um die Überführungsfunktion des DFA zu definieren, werden alle Zustände in der aktuellen Menge \(M\) für ein Symbol \(x\) durchgegangen und für jeden dieser Zustände die Menge der möglichen Nachfolgezustände im NFA ermittelt. Alle diese Mengen werden dann vereinigt und ergeben den Nachfolgezustand im DFA.



Mit dem Zustand \(\{z_0\}\) sind wir nun fertig, aber wir haben einen neuen Zustand generiert und machen mit diesem wie eben weiter. Wir halten also ein Symbol \(x\) des Eingabealphabets fest, gehen dann bei \(\{z_0,z_1\}\) alle Zustände durch, ermitteln im NFA die Menge der Nachfolgezustände von \(x\), also \(\delta(z_0,x)\) und \(\delta(z_1,x)\), und vereinigen diese Mengen. Die sich so ergebene Menge ist der Nachfolgezustand im DFA für das Symbol \(x\).



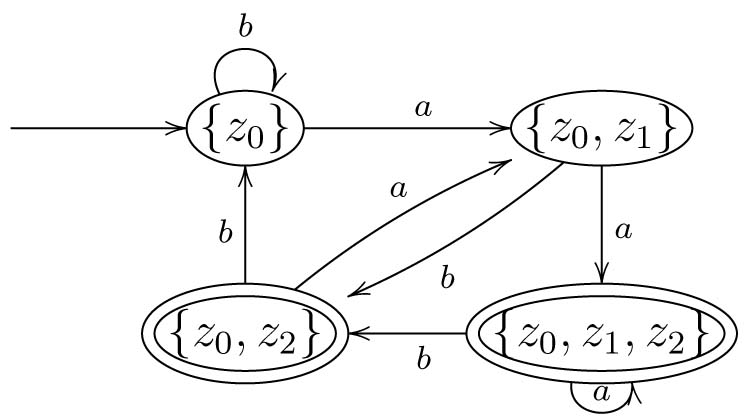
Dies schließt die Konstruktion ab. Wir hätten streng nach der angegebenen Konstruktion noch weitere Zustände konstruieren müssen, die aber für die akzeptierte Sprache nicht von Bedeutung sind, da sie vom Startzustand aus nicht erreicht werden können. Wir kommen auf diesen Unterschied später noch einmal zu sprechen.
Beweis (Fortsetzung)
Nach diesem Beispiel setzen wir den Beweis nun fort. Wir wollen jetzt \(L(A) = L(B)\) zeigen. Da wir dies gleich im Beweis brauchen werden, wiederholen wir noch einmal die Definitionen für die erweiterte Überführungsfunktion und die akzeptierte Sprache jeweils für DFAs und NFAs. Bei dem DFA benutzen wir die gestrichene Variante (also \(\hat{\delta}‘\)) und passen auch ansonsten die Definition auf die Bezeichnungen in der hiesigen Konstruktion an. Wir haben dann:\(\begin{eqnarray*}
\hat{\delta}(M, \lambda) & := & M \\
\hat{\delta}(M, xw) & := & \hat{\delta}(\cup_{z \in M} \delta(z,x),w) \\
\hat{\delta}'(M, \lambda) & := & M \\
\hat{\delta}'(M, xw) & := & \hat{\delta}'(\delta'(M,x),w)
\end{eqnarray*}\)
\(\begin{eqnarray*}
L(A) & := & \{w \in \Sigma^* \mid \hat{\delta}(Z_{start}, w) \cap Z_{end} \not= \emptyset \} \\
L(B) & := & \{w \in \Sigma^* \mid \hat{\delta}'(z_0, w) \in Z_{end}‘ \}
\end{eqnarray*}\)
Wenn man noch bedenkt, dass in der Konstruktion \(\delta'(M,x) := \cup_{z \in M} \delta (z,x)\) gesetzt wird, dann sehen die erweiterten Überführungsfunktionen fast identisch aus. Ebenso sehen die akzeptierten Sprachen fast identisch aus, wenn man die Definition von \(Z_{end}‘\) und \(z_0\) beachtet. Diese \“Ahnlichkeit ist gerade der Ursprung für die folgende Beweisidee. Statt \(L(A) = L(B)\) durch Teilmengenbeziehungen direkt zu zeigen, zeigen wir per Induktion über die Wortlänge \(|w|\), dass für jedes \(w \in \Sigma^*\) und \(M \subseteq Z\) $$ \hat\delta'(M,w) = \hat\delta(M,w) $$ gilt. Wir zeigen also, dass wir nach Lesen eines Wortes \(w\) in der gleichen Menge von Zuständen sind, also im NFA in einer Menge von Zuständen, die besagt, dass wir in diesen Zuständen nichtdeterministisch sind und im DFA in einem Zustand, der aber gerade diese gleiche Menge von Zuständen ist. (Man kann sich schon hier überlegen, dass dies dann genügt, um zu zeigen, dass beide Automaten die gleichen Worte und damit letztendlich die gleiche Sprache akzeptieren. Denn wenn diese Mengen gleich sind, dann ist in beiden entweder ein Endzustand des NFA oder eben nicht. Damit akzeptieren aufgrund der Akzeptanzbedingungen und der Konstruktion gerade beide Automaten oder eben nicht.)
Induktionsanfang: \(|w| = 0\), d.h. \(w = \lambda\). In diesem Fall ist \(\hat\delta'(M,w) = \hat\delta(M, w) = M\) (wegen der Definition der erweiterten Überführungsfunktion).
Induktionsannahme: Gelte die Induktionsbehauptung für Worte der Länge \(n \geq 0\).
Induktionsschritt: Sei nun \(w \in \Sigma^*\) mit \(|w| = n+1\). Wir zerlegen \(w\) in \(xv\) (also \(w = xv\)) mit \(x \in \Sigma\). \(x\) ist also das erste Symbol. Nach den Definitionen der erweiterten Überführungsfunktionen folgt nun
- \(\hat{\delta}(M, xv) = \hat{\delta}(\cup_{z \in M} \delta(z,x), v)\)
- \(\hat{\delta‘}(M, xv) = \hat{\delta‘}(\delta'(M,x),v) = \hat{\delta‘}(\cup_{z \in M} \delta(z,x), v)\)
Die letztere Gleichheit folgt dabei aufgrund der Definition von \(\delta‘\) in der Konstruktion. Setzen wir zur einfacheren Notation noch \(\cup_{z \in M} \delta(z,x) =: M‘\), dann haben wir in den beiden Zeilen ganz rechts also \(\hat{\delta}(M‘, v)\) und \(\hat{\delta‘}(M‘, v)\). Nun gilt aber \(|v| = n\) und damit ist die Induktionsannahme anwendbar, d.h. es ist \(\hat{\delta}(M‘, v) = \hat{\delta}'(M‘, v)\) und damit sind oben die beiden Zeilen gleich und wir haben also \(\hat{\delta}(M, xv) = \hat{\delta‘}(M, xv)\) bzw. mit \(w = xv\) dann \(\hat{\delta}(M, w) = \hat{\delta}'(M, w)\).
Damit ist die Induktionsbehauptung gezeigt. Setzen wir zum Abschluss des Beweises nun für \(M\) die Menge \(Z_{start}\) bzw. \(z_0\) ein (was nach Konstruktion das gleiche ist), so erhalten wir
$$ \hat\delta'(z_0, w) = \hat\delta(Z_{start},w). $$
Nach Konstruktion und Definition der Akzeptanzbedingungen akzeptiert nun der NFA \(A\) genau dann, wenn \(\hat\delta(Z_{start},w) \cap Z_{end} \not= \emptyset\) und der DFA \(B\) genau dann, wenn \(\hat\delta'(z_0, w) \in Z_{end}‘\) d.h. nach Konstruktion wenn \(\hat\delta'(z_0, w) \cap Z_{end} \not= \emptyset\) gilt. Wegen \(\hat\delta'(z_0, w) = \hat\delta(Z_{start},w)\) akzeptieren also sowohl \(A\) als auch \(B\) ein Wort \(w\) oder lehnen es beide ab. Daraus folgt \(L(A) = L(B)\).
Damit haben wir gezeigt, dass wir zu jedem NFA einen DFA konstruieren können, der die gleiche Sprache akzeptiert. Da die Menge der Zustände des DFA gerade die Potenzmenge der Zustände des NFA ist, wird diese Konstruktion Potenzautomatenkonstruktion und der entstehende DFA der Potenzautomat (zu dem NFA) genannt.
Man spricht in diesem Fall von der Äquivalenz der beiden Automatenmodelle. Allgemein sagt man, dass, wenn zwei DFAs \(A_1\) und \(A_2\) die gleiche Sprache akzeptieren, wenn also \(L(A_1) = L(A_2)\) gilt, dass dann \(A_1\) und \(A_2\) äquivalent sind. Ebenso spricht man dann auch bei zwei Automaten unterschiedlicher Automatenmodelle davon, dass sie äquivalent sind, wenn sie die gleiche Sprache akzeptieren. Und letztendlich spricht man in dem Fall, dass es so wie hier möglich ist, zu jedem Automaten eines speziellen Modells einen äquivalenten Automaten eines anderen speziellen Modells zu konstruieren, davon, dass die Automatenmodelle äquivalent sind. NFAs und DFAs sind also äquivalente Automatenmodelle oder kürzer: äquivalent.
- einen DFA \(A\) mit \(L(A) = L\) und
- einen NFA \(B\) mit \(L(B) = L\).
Zum Abschluss noch der Hinweis auf den Unterschied in der Konstruktion im Beweis und im Vorgehen im Beispiel. In der Konstruktion im Beweis wurde \(Z‘ := 2^Z\) gesetzt. Im Beispiel haben wir nur die initiale Zusammenhangskomponente konstruiert. Letzteres genügt stets, d.h. man könnte die Konstruktion im Beweis so umformulieren, dass man sie algorithmisch formuliert und bei \(z_0 := Z_{start}\) beginnt und dann (so wie im Beispiel) nach und nach weitere, erreichbare Zustände (also insgesamt die initiale Zusammenhangskomponente) generiert. Der Korrektheitsbeweis geht dann ganz genauso. Die Aussagen bleiben also die gleichen, bei der Ausführung oder Implementierung ist die Variante mit der initialen Zusammenhangskomponente aber meist schneller und platzsparender. In der Konstruktion im Beweis wurde hier die eher statische Variante gewählt, um die Potenzmenge deutlich sichtbar zu machen.
Tatsächlich gibt es auch Fälle, in denen alle Zustände der Potenzmenge nötig sind, d.h. es gibt Fälle, in denen der DFA exponentiell mehr Zustände benötigt als der DFA ([/latex]2^{|Z|}[/latex] im Vergleich zu \(|Z|\)). In den meisten Fällen werden zwar nicht alle gebraucht, es gibt aber eben doch Beispiele, wo diese Zahl erreicht wird und tatsächlich auch nötig ist, d.h. die hohe Zahl ist auch keine Schwäche der Konstruktion!
Eine gute Näherung für diesen Fall hat man schon mit dem Automaten, bei dem das drittletzte Symbol ein bestimmter Buchstabe sein muss bzw. mit Verallgemeinerungen davon.
Ein äquivalenter DFA für diese Sprache hat bereits mindestens \(2^{n-1}\) Zustände.

Wir wollen noch diesen und den vorangegangenen Abschnitt zusammenfassen. Zunächst haben wir nichtdeterministische endliche Automaten (NFA) als Verallgemeinerung der DFAs eingeführt. Die hauptsächliche Änderung war, dass zu einem Zustand und einem Symbol nun mehr als ein Nachfolgezustand existieren darf. Zusätzlich wurde auch angepasst, dass der NFA auch gleich zu Beginn in mehr als einem Startzustand sein kann. Anschließend haben wir dann wo nötig die Definitionen des DFA angepasst. Wir passten also die Definition der erweiterten Überführungsfunktion an und übertrugen auch die Begriffe Konfiguration, Konfgurationsübergang, Rechnung und Erfolgsrechnung auf NFAs. Zuletzt passten wir dann die Definition der akzeptierten Sprache an.
In diesem Abschnitt haben wir dann mit der Potenzautomatenkonstruktion eine Konstruktion kennengelernt, die es uns ermöglicht zu jedem beliebigen NFA einen DFA zu konstruieren, der die gleiche Sprache akzeptiert. Die beiden Automatenmodelle sind also äquivalent und erfassen beide die Familie der regulären Sprachen. Im Beweis der Potenzautomatenkonstruktion haben wir wieder einen induktiven Beweis über die Wortlänge gesehen.
Nachdem wir also den NFA eingeführt haben, haben wir gleich gesehen, dass er gar nicht nötig ist, um wirklich neue Dinge tun zu können. Er ist aber dennoch sehr nützlich, da er es uns erlaubt in vielen Fällen eine viel kompaktere Darstellung für eine reguläre Sprache zu haben, als dies mit DFAs möglich ist. Zudem führten wir mit ihm das Konzept des Nichtdeterminismus ein, das uns später noch oft begegnen wird und sich als sehr nützlich erweisen wird.
