Den in der Definition der Syntax beschriebenen Aufbau komplexer Formeln aus einfache(re)n Formeln kann man nutzen, um Funktionen über die Formelmenge zu definieren und so bspw. eine Funktion \(f\) zu definieren, die jeder Formel \(F\) einen Wert \(f(F)\) zuzuweisen (bspw. die Länge der Formel oder die Anzahl der Junktoren in der Formel). Man nennt dies strukturelle Rekursion).
Ähnlich kann man den Aufbau der Formeln auch nutzen, um Eigenschaften von Formeln nachzuweisen. Dies wird als strukturelle Induktion bezeichnet und wird im nächsten Abschnitt behandelt.
Wenn wir nun mittels struktureller Rekursion eine Funktion definieren wollen, so ist es unser Ziel eine (totale) Funktion \(f: \mathcal{L}_{AL} \rightarrow D\) zu definieren, wobei \(D\) dabei eine beliebige Menge sein kann. \(f\) wird also jeder Formel \(F \in \mathcal{L}_{AL}\) ein Element \(x \in D\) zuweisen. In unserem Fall wird \(D\) meist die Menge \(\mathbb{N}\) der natürlichen Zahlen sein. Um \(f\) nun zu definieren genügt es,
- \(f(A)\) für jedes \(A \in AS_{AL}\) festzulegen und
- eine Funktion \(f_\neg : D \rightarrow D\) und für jeden Junktor \(\circ \in \{\vee, \wedge, \Rightarrow, \Leftrightarrow\}\) eine Funktion \(f_\circ: D \times D \rightarrow D\) zu definieren.
Es ist dann \(f(\neg F) := f_\neg(f(F))\) und z.B. \(f((F \wedge G)) := f_\wedge(f(F), f(G))\) (und analog für die anderen zweistelligen Junktoren).
Die Definition oben erscheint zunächst vielleicht kompliziert. Betrachten wir sie einmal genauer. Zunächst legt man sich auf eine Menge \(D\) fest auf die man abbilden will. Will man z.B. jeder Formel einen Zahlenwert zuweisen? Oder einen Buchstaben? Oder vielleicht eine andere Formel? Wir arbeiten nachfolgend mit Zahlenwerten, also k\"onnen wir ruhig mit \(D = \mathbb{N}\) arbeiten. Zunächst muss dann also für jedes Aussagensymbol \(A \in AS_{AL}\) eine Zahl \(f(A) \in \mathbb{N}\) festgelegt werden (denn \(f\) bildet ja jetzt auf \(D = \mathbb{N}\) ab). Setzen wir einmal \(f(A) = 1\) für jedes \(A \in AS_{AL}\) (man könnte auch verschiedenen Aussagensymbolen verschiedene Werte aus \(\mathbb{N}\) zuweisen, wichtig ist nur, dass jedem Aussagensymbol ein Wert aus \(\mathbb{N}\) zugewiesen wird). Dies wird als Rekursionsbasis bezeichnet.
Im zweiten Schritt wird dann verlangt, dass zunächst eine Funktion \(f_\neg\) definiert wird, die eine natürliche Zahl nimmt und auf eine andere abbildet. Statt dann für z.B. \(\neg A\) und \(\neg B\) explizit \(f(\neg A)\) und \(f(\neg B)\) festzulegen kann man dann die eben festgelegte Rekursionsbasis (die definiert ja u.a. die Werte \(f(A)\) und \(f(B)\)) und die Funktion \(f_\neg\) benutzen und so \(f(\neg A) = f_\neg(f(A))\) bzw. \(f(\neg B) = f_\neg(f(B))\) zu bestimmen. Dies hat neben dem eben genannten Vorteil, dass man deutlich weniger definieren muss, zudem den Vorteil, dass sich die Werte \(f(F)\) für komplexe Formeln \(F\) aus den Werten (unter \(f\)) für Teilformeln von \(F\) ergibt. Ist z.B. \(F\) eine Konjunktion \(F = G \wedge H\), so ermittelt sich \(f(F)\) aus den Werten \(f(G)\) und \(f(H)\), die man dann beide als Argumente von \(f_\wedge\) nutzt. Man bezeichnet die Definition von \(f_\neg\) und der \(f_\circ\) für die zweistelligen Junktoren \(\circ\) als Rekursionsschritt. Man beachte, dass die zweistelligen Junktoren nicht alle gleich behandelt werden müssen.
Zusammenfassend: Will man eine Funktion \(f\) definieren, die jeder Formel \(F\) der Aussagenlogik ein Element aus einer Menge \(D\) zuweist (z.B. einen Zahlenwert aus \(\mathbb{N}\)), so genügt es zunächst \(f\) auf allen atomaren Formeln zu definieren (häufig ist dieser Wert für alle atomaren Formeln gleich). Im Anschluss definiert man dann noch, was passieren soll, wenn man auf einen der Junkotren trifft, d.h. man definiert wie sich der Wert von z.B. \(f(F \wedge G)\) aus den Werten \(f(F)\) und \(f(G)\) ergibt (z.B. k\"onnte man \(f(F \wedge G) = f(F) + f(G) + 3\) setzen, womit man implizit \(f_\wedge(n,m) = n+m+3\) definiert). Unten folgen als Beispiele die Definitionen von Grad und Tiefe. Dort wird (wie meist üblich) in der Rekursionsbasis für alle Aussagensymbole der gleiche Wert genommen und (wie nicht umbedingt üblich aber doch häufig anzutreffen) die Funktionen aller zweistelligen Junktoren stimmen überein.
Damit ist es z.B. möglich den Grad und die Tiefe einer Formel zu definieren.
Definition 2.2.1
Die Funktionen \(grad: \mathcal{L}_{AL} \rightarrow \mathbb{N}\) und \(tiefe: \mathcal{L}_{AL} \rightarrow \mathbb{N}\) werden wie folgt definiert:- Für jedes \(A \in AS_{AL}\) sei
- \(grad(A) = tiefe(A) = 0\).
- Für \(\neg\) sei
- \(grad(\neg F) = grad_\neg(grad(F)) = grad(F) + 1\) und
- \(tiefe(\neg F) = tiefe_\neg(tiefe(F)) = tiefe(F) + 1\).
- (Oder anders: \(grad_\neg : \mathbb{N} \rightarrow \mathbb{N}\) wird definiert durch \(grad_\neg(n) = n + 1\) und entsprechend für \(tiefe_\neg\).
- Für \(\circ \in \{\vee, \wedge, \Rightarrow, \Leftrightarrow\}\) sei
- \(grad((F \circ G)) = grad_\circ(grad(F), grad(G)) = grad(F) + grad(G) + 1\) und
- \(tiefe((F \circ G)) = tiefe_\circ(tiefe(F), tiefe(G)) = max(tiefe(F), tiefe(G)) + 1\).
Für eine Formel \(F\) ist \(grad(F)\) dann der Grad der Formel \(F\) und \(tiefe(F)\) die Tiefe der Formel \(F\).
Informal formuliert ist der Grad einer Formel die Anzahl der Junktoren (bei \(((A \wedge (B \Rightarrow C)) \vee (B \wedge A))\) also \(4\)). Die Tiefe einer Formel ist die Anzahl der Junktoren in der tiefsten Verschachtelung. Führt man noch Strukturbäume ein, so kann man die Tiefe verstehen als die Anzahl der Junktoren auf dem längsten Pfad im Strukturbaum.
Statt Formeln als Zeichenketten der Art \((A \wedge B)\) auszudrücken, kann man Formeln auch als Bäume, sogenannte Strukturbäume, ausdrücken. Dies ist für manche Algorithmen hilfreich.
Ein Strukturbaum zu einer Formel \(F\) ist ein Baum, bei dem die inneren Knoten (die Knoten, die keine Blätter sind) Junktoren sind und die Blätter die atomaren (Teil-)Formeln von \(F\).
Im einzelnen:
- Der Hauptoperator markiert die Wurzel.
- Teilformeln entsprechen Teilbäumen.
- Die Reihenfolge der Teilformeln wird beibehalten (linke Teilformel, linkes Kind).
- Die Aussagesymbole werden dann die Blätter des Baumes.
- Die Junktoren sind die inneren Knoten. Dabei hat \(\neg\) ein Kind, alle anderen Junktoren haben zwei Kinder.
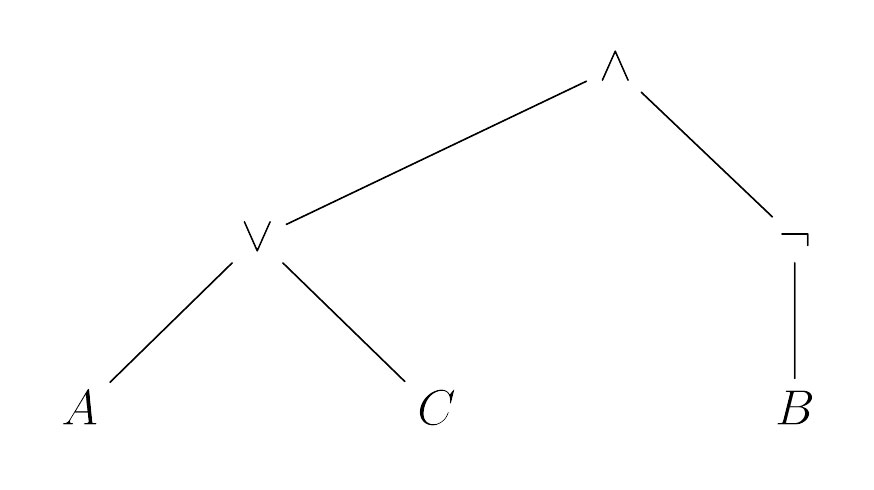
Ein Beispiel veranschaulicht dies schnell. Sei \(F = ((A \vee C) \wedge \neg B)\), dann ergibt sich als Strukturbaum zu \(F\)