Der DFA

Download PDF

 
Nach den Vorarbeiten des letzten Abschnittes sind wir nun in der Lage den deterministischen endlichen Automaten formal einzuführen. Wir erinnern noch einmal an die Überlegung, die wir in der Einleitung angestellt haben. Wichtig für den endlichen Automaten war, dass

  • wir ein System mit einer endlichen Anzahl von Zuständen haben,
  • von denen einer als Startzustand und
  • eine beliebige Teilmenge als Endzustände hervorgehoben sind,
  • dass Zustandsübergänge möglich sind und
  • dass das System sich stets in genau einem Zustand befindet.

Formal können wir dies wie folgt exakt beschreiben.

Definition 2.1.2 (Deterministischer endlicher Automat (DFA))

Ein deterministischer, endlicher Automat (DFA) ist ein \(5\)-Tupel
$$ A = (Z, \Sigma, \delta, z_0, Z_{end}) $$
mit:

  1. Der endlichen Menge von Zuständen \(Z\).
  2. Dem endlichen Alphabet \(\Sigma\) von Eingabesymbolen.
  3. Der Überführungsfunktion \(\delta: Z \times \Sigma \rightarrow Z\).
  4. Dem Startzustand \(z_0 \in Z\).
  5. Der Menge der Endzustände \(Z_{end} \subseteq Z\).


Als graphische Darstellung wählen wir Kreise für die Zustände und notieren die Bezeichnung des Zustandes meist im Kreis. Der Startzustand wird mit einer eingehenden Kante ohne Ursprung notiert, Endzustände mit Doppelkreisen. Die Überführungsfunktion wird mit beschrifteten, gerichteten Kanten notiert. Ist bspw. \(\delta(z,a) = z‘\), so gibt es eine gerichtete Kante von \(z\) nach \(z‘\), die mit \(a\) beschriftet ist. Ein Beispiel ist der abgebildete Automat:
Mit den Zustandsmenge \(Z = \{z_0, z_1\}\), dem Startzustand \(z_0\), der Endzustandsmenge \(Z_{end} = \{z_1\}\) und der Überführungsfunktion \(\delta\), die durch \(\delta(z_0, 0) = z_0\), \(\delta(z_0, 1) = z_1\) und \(\delta(z_1, 0) = z_1\) gegeben ist. (Man beachte, dass \(\delta(z_1, 1)\) nicht definiert ist. Die Funktion \(\delta\) muss nicht total sein und wir werden gleich sagen, dass der Automat in solchen Fällen blockiert.) Sofern nicht anders erwähnt ist das Eingabealphabet \(\Sigma\) die Menge der Symbole, die als Kantenbeschriftungen benutzt werden. Im abgebildeten Beispiel wäre also \(\Sigma = \{0,1\}\). Eine solche graphische Darstellung eines DFA \(A\) wird als Zustandsübergangsdiagramm von \(A\) bezeichnet.

Dies beschreibt nun zunächst nur die Struktur eines DFA. Um auch seine Dynamik, d.h. sein Verhalten beschreiben zu können. Machen wir uns zunächst noch einmal informal klar, wie ein DFA arbeiten soll. Die Eingabe für einen DFA \(A = (Z, \Sigma, \delta, z_0, Z_{end})\) ist ein Wort aus \(\Sigma^*\). Sei dieses Wort mit \(w\) bezeichnet (also \(w \in \Sigma^*\) ist \(\Sigma = \{a,b\}\), so könnte \(w\) z.B. \(abbb\) sein). \(A\) arbeitet dann wie folgt:

  1. \(A\) beginnt im Startzustand \(z_0\).
  2. Beginnt \(w\) mit dem Symbol \(x \in \Sigma\),
  3. so wird der Nachfolgezustand nun durch \(\delta(z_0, x)\) bestimmt.
  4. Dies wird dann in dem nun aktuellen Zustand und mit dem Restwort fortgeführt (ist \(A\) also z.B. nun in \(z\) und ist der nächste Buchstabe ein \(y\), so ist der Nachfolgezustand \(\delta(z,y)\) usw.)
  5. Das Wort \(w\) wird akzeptiert, wenn
    • \(w\) bis zum Ende gelesen werden kann und
    • der Automat dann in einem Endzustand ist.

Das Wort wird nicht akzeptiert, wenn der Automat entweder nach Lesen des Wortes nicht in einem Endzustand ist oder wenn das Wort nicht zu Ende gelesen werden kann. Letzteres passiert, wenn er in einem Zustand \(z\) ist und das Symbol \(x\) als nächstes gelesen werden soll, es aber keinen Nachfolgezustand gibt, d.h. wenn \(\delta(z,x)\) nicht definiert ist (oder im Diagramm: wenn es keine Kante aus \(z\) heraus gibt, die mit \(x\) beschriftet ist).

 


Betrachten wir das Beispiel aus Abbildung 2.4. Der Startzustand ist \(z_0\) (markiert durch den eingehenden Pfeil), der einzige Endzustand ist \(z_2\) (markiert durch die doppelten Kreise). Die Werte von \(\delta\) werden durch die Kantenrichtungen und Kantenbeschriftungen ausgedrückt, bspw. ist \(\delta(z_0, a) = z_1\) und \(\delta(z_0, b)\) nicht definiert (beginnt ein Wort also mit \(b\) kann der Automat dieses Wort nicht akzeptieren, da er es nicht zu Ende lesen kann).

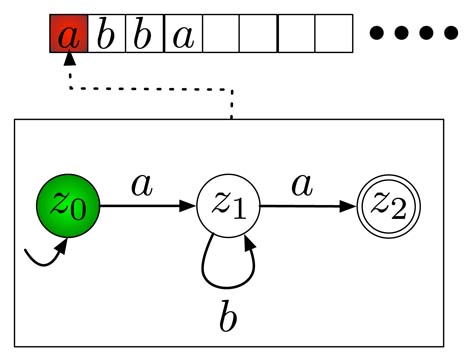
DFA mit Eingabewort.
2.4: DFA mit Eingabewort \(abba\).

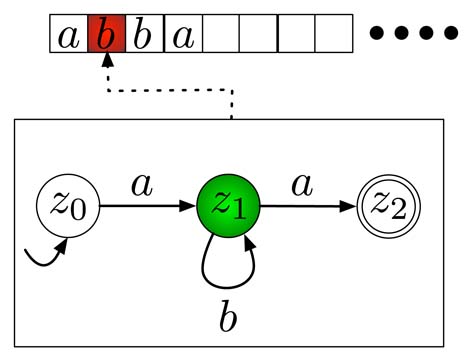
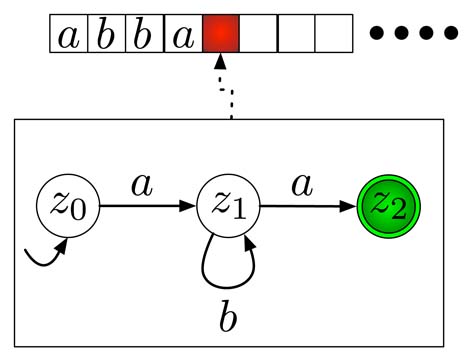
Im Beispiel der Abbildung mit dem Wort \(abba\) wird nun zuerst das \(a\) gelesen und dabei der Zustandswechsel nach \(z_1\) gemacht (Abbildung 2.5). Dort können dann mittels der \(b\)-Schleife die beiden \(b\) gelesen werden und im Anschluss wird mit der \(a\)-Kante von \(z_1\) nach \(z_2\) in den Zustand \(z_2\) gewechselt (Abbildung 2.6).

Da \(z_2\) nun ein Endzustand ist und das Wort zu Ende gelesen wurde, wird \(abba\) akzeptiert. In Fällen, in denen der Automat bei einem Wort nicht diese beiden Bedingungen erfüllt, wird das Wort nicht akzeptiert.


DFA nach Lesen.
2.5: DFA nach Lesen des ersten \(a\).


DFA nach Lesen.
2.6: DFA nach Lesen des ganzen Wortes.

Akzeptieren und Ablehnen von Worten

Um es zu betonen: Ein Wort \(w\) wird von einem DFA \(A\) akzeptiert, wenn der Automat das Wort bis zum Ende lesen kann (also nie der Fall auftritt, dass \(A\) in einem Zustand \(z\) ist, den nächsten Buchstaben \(x\) des Wortes aber nicht lesen kann, da \(\delta(z,x)\) nicht definiert ist) und dann in einem Endzustand ist.

Im Beispiel wird das Wort \(abba\) akzeptiert, da beide Bedingungen zutreffen.

Das Wort \(abb\) wird bspw. nicht akzeptiert, da das Wort zwar zu Ende gelesen werden kann, der Automat dann aber immer noch in \(z_1\) ist und \(z_1\) kein Endzustand ist. Das Wort \(ba\) wird nicht akzeptiert, da der Automat in \(z_0\) das \(b\) nicht lesen kann (der Übergang \(\delta(z_0,b)\) ist nicht definiert). Das Wort \(aab\) wird nicht akzeptiert, da der Automat nach \(aa\) zwar in dem Endzustand \(z_2\) ist, das Wort dann aber noch nicht zu Ende gelesen ist (und auch nicht mehr zu Ende gelesen werden kann, da \(\delta(z_2, b)\) nicht definiert ist).

Zuletzt sei betont, dass beide Bedingungen gleichzeitig eintreten müssen: das Wort muss zu Ende gelesen sein und der Automat muss dann in einem Endzustand sein. Ist im Beispiel \(z_1\) ein Endzustand und \(z_2\) kein Endzustand, so würde bspw. \(aa\) nicht akzeptiert werden. Nach Lesen von \(a\) ist der Automat zwar in \(z_1\), was ja jetzt ein Endzustand ist, hat das Eingabewort \(aa\) aber noch nicht zu Ende gelesen. Mit dem zweiten \(a\) verlässt der Automat den Zustand \(z_1\) dann wieder und wechselt nach \(z_2\), was nun ja aber kein Endzustand ist. Das Wort \(aa\) ist dann zwar zu Ende gelesen, aber der Automat ist nun in \(z_2\) und akzeptiert nicht. Wichtig ist also nicht, dass irgendwann einmal ein Endzustand besucht wurde, sondern dass der Automat das Wort zu Ende gelesen hat und dann in einem Endzustand ist.


 
Bevor wir die von einem Automaten akzeptierten Wörter und damit die akzeptierte Sprache formal einführen, erweitern wir zunächst noch die Überführungsfunktion \(\delta\) und führen den Begriff der Konfiguration und der Erfolgsrechnung ein. Die letzteren beiden Begriffen werden meist erst für komplexere Automatenmodelle eingeführt, aber es ist eine gute Übung sie bereits hier einzuführen.

Definition 2.1.3 (Erweiterte Überführungsfunktion)

Sei \(A = (Z, \Sigma, \delta, z_0, Z_{end})\) ein DFA. Die erweiterte Überführungsfunktion \(\hat{\delta}: Z \times \Sigma^* \rightarrow Z\) wird für alle \(z \in Z\), \(x \in \Sigma\) und \(w \in \Sigma^*\) rekursiv definiert durch

\(\hat{\delta}(z, \lambda) := z\)
\(\hat{\delta}(z, xw) := \hat{\delta}(\delta(z,x),w)\).

Beispiel Überführungsfunktion

Sei \(A\) durch folgendes Zustandsübergangsdiagramm gegeben. Dann ist \(\hat{\delta}(z_0, 001) = \hat{\delta}(z_0, 01) = \hat{\delta}(z_0, 1) = z_1\) und abkürzend schreibt man dann einfach \(\hat{\delta}(z_0, 001) = z_1\) oder bricht an einer beliebigen für einen interessanten Stelle ab.

 

Definition 2.1.4 (Konfiguration und Rechnung)

  1. Eine Konfiguration eines DFA \(A\) ist ein Tupel \((z,w) \in Z \times \Sigma^*\) mit der Bedeutung, dass \(A\) im Zustand \(z\) ist und noch das Wort \(w\) zu lesen ist.
  2. Ein Konfigurationsübergang ist dann $$(z,w) \vdash (z‘,v)$$ genau dann, wenn \(w = xv\), \(x \in \Sigma\) und \(\delta(z,x) = z‘\) ist.
  3. Eine Rechnung auf dem Wort \(w \in \Sigma^*\) ist eine Folge von Konfigurationsübergängen, die in \((z_0, w)\) beginnt.
  4. Endet die Rechnung in \((z‘, \lambda)\) und ist \(z‘ \in Z_{end}\), so ist dies eine Erfolgsrechnung und \(w\) wird akzeptiert.

Beispiel Konfiguration und Rechnung

Sei wieder \(A\) durch folgendes Zustandsübergangsdiagramm gegeben. Dann ist bei Eingabe \(001\) die Konfiguration zu Beginn \((z_0, 001)\). Auf diesem Wort hat der Automat die Rechnung $$(z_0, 001) \vdash (z_0, 01) \vdash (z_0, 1) \vdash (z_1, \lambda)$$ Da die Rechnung in \((z_1, \lambda)\) endet und \(z_1\) ein Endzustand ist, ist dies sogar eine Erfolgsrechnung.

 
Damit können wir nun formal den wichtigen Begriff der akzeptierten Sprache eines DFA definieren und damit die Sprachfamilie der regulären Sprachen.

Definition 2.1.5 (Akzeptierte Sprache)

Die von einem DFA \(A\) akzeptierte Sprache ist die Menge

\(\begin{eqnarray*}
L(A) & := & \{w \in \Sigma^* \mid \hat{\delta}(z_0, w) \in Z_{end}\} \\
& = & \{w \in \Sigma^* \mid (z_0, w) \vdash^* (z_e, \lambda), z_e \in Z_{end}\}
\end{eqnarray*}\)

Eine von einem DFA akzeptierte Sprache wird auch als reguläre Menge bezeichnet und die Familie aller regulären Mengen wird mit \(REG\) bezeichnet.

Man beachte, wie unsere obige intuitive Beschreibung von der Definition erfasst wird. In \(L(A)\) sind genau jene Worte, die von \(A\) zu Ende gelesen werden können und die \(A\) dabei vom Startzustand \(z_0\) in einen Endzustand überführen.

Hinweis zur akzeptierten Sprache eines DFA

Sei noch einmal betont, dass in \(L(A)\) genau die Worte sind, die von \(A\) akzeptiert werden, nicht mehr und nicht weniger. Wenn wir später also behaupten, dass in einer Menge \(M\) gerade die Worte sind, die von einem Automaten \(A\) akzeptiert werden, dann behaupten wir also \(L(A) = M\) (und müssen dies dann noch beweisen). Wir kommen darauf gleich noch zu sprechen, aber man mache sich noch einmal jetzt schon klar, dass in \(L(A)\) exakt die Worte enthalten sind, die \(A\) akzeptiert, nicht weniger, nicht mehr. Soll man also z.B. einen Automaten konstruieren, der alle Worte akzeptiert, die mit \(a\) beginnen, so muss man darauf achten, dass man alle Worte mit dieser Eigenschaft akzeptiert und nicht weniger - aber eben auch nicht mehr.

 

Zuletzt noch zwei Begriffe, die im Zusammenhang mit endlichen Automaten sowohl bei der Konstruktion als auch bei Beweisen öfter auftreten.

Definition 2.1.6

Ein DFA \(A = (Z, \Sigma, \delta, z_0, Z_{end})\) heißt

  1. vollständig, wenn zu jedem \((z,x) \in Z \times \Sigma\) ein \(z‘\) existiert mit \(\delta(z,x) = z‘\).
  2. initial zusammenhängend, wenn es zu jedem \(z \in Z\) ein Wort \(w\) gibt mit \(\hat{\delta}(z_0,w) = z\).

Ist ein Automat vollständig, so gibt es also zu jedem Symbol des Eingabealphabets eine Kante in jedem Zustand. Dies führt dazu, dass jede Eingabe (zu Ende) gelesen werden kann. Initial zusammenhängend bedeutet, dass jeder Zustand erreichbar ist. Dies ist bisweilen gut zu wissen, da die anderen Zustände im Grunde nutzlos sind. Man spricht auch von einer initialen Zusammenhangskomponente, wenn man die Zustände meint, die vom Startzustand aus erreichbar sind und schränkt einen DFA oft auf diese ein.

 

Wichtige Begriffe

Wichtige Begriffe bis hierhin waren zu den formalen Sprachen die Begriffe Alphabet, Konkatenation, Wort, leeres Wort und die Notationen \(R^+\), \(R^*\), \(\Sigma^+\), \(\Sigma^*\), \(R^0\), \(R^1\), \(R^i\), \(w^0\), \(w^1\), \(w^i\), sowie zu den endlichen Automaten die Begriffe DFA, Zustände, Startzustand, Endzustände, Überführungsfunktion, erweitere Überführungsfunktion, vollständig, initial zusammenhängend, Konfiguration, Konfigurationsübergang, Rechnung, Erfolgsrechnung, akzeptierte Sprache, reguläre Menge und die Sprachfamilie REG. Alle diese Begriffe sind wichtig und sollten bekannt sein, da wir auf ihrer Grundlage aufbauen und einem sonst im weiteren Verlauf wichtige Vokabeln fehlen. Daher diese Begriffe ruhig noch einmal angucken.

 
 

Hier ein paar Fragen zu DFAs.