Bisher haben wir die deterministische Turingmaschine mit einem beidseitig unendlichem Band kennengelernt. Man kann viele Varianten der Turingmaschine einführen, von denen einige recht nützlich beim Entwurf einer Turingmaschine für eine bestimmte Sprache oder eine bestimmte Funktion sind. Wir werden nachfolgend zwei Varianten der deterministischen Maschine einführen. Die eine hat nur ein einseitig unendliches Band, die andere hat mehrere Bänder. Wir werden sehen, dass diese Maschinen äquivalent sind und können dann also je nach Fragestellung die benutzen, die uns am sinnvollsten erscheint. Äquivalent bedeutet dabei wieder, dass es zu jeder TM des einen Typs eine TM des anderen Typs gibt, so dass die gleichen Sprachen akzeptiert werden.
Definiton 4.2.1
Zwei Turingmaschinen \(A\) und \(B\) sind äquivalent, wenn \(L(A) = L(B)\) gilt.Im Anschluss werden wir dann so wie wir es auch bei endlichen Automaten gemacht haben noch eine nichtdeterministische Variante der Turingmaschine einführen.
Nutzung verschiedener Bänder
Die bisherige DTM hat ein Band, das in beide Richtungen unendlich ist (ein beidseitig unendliches Band). Man kann eine TM definieren, bei der das Band nur in eine Richtung unendlich ist. Diese TM startet dann in einer Konfiguration \(z_0 w\) und kann das Band nicht nach links verlassen. Nach rechts hin ist das Band aber unendlich.
Definiton 4.2.2
aEine DTM mit einem einseitig unendlichem Band ist wie eine DTM mit einem zweiseitig unendlichem Band definiert, kann das Band aber nicht von der anfänglichen Startposition nach links verlassen. Nummeriert man die Zellen des Bandes durch und nennt die erste Zelle die \(0\)te Zelle, so kann diese Zelle nicht nach links verlassen werden (die späteren Zellen aber schon).Es wäre nun noch die Schrittrelation anzupassen, was dadurch verkompliziert wird, dass das Band nicht nach links verlassen werden kann. Wir wollen dies hier nicht im Detail machen. Ein intuitives Verständnis dieser Maschinen genügt uns an dieser Stelle.
Dass die DTM mit einem beidseitig unendlichem Band alles kann, was die DTM mit einem einseitig unendlichem Band kann, ist wenig überraschend. Andersherum geht dies aber auch. Die beiden Formalismen sind also äquivalent.
Satz 4.2.3
Zu jeder DTM \(A\) mit einseitig unendlichem Band gibt es eine äquivalente DTM \(B\) mit beidseitig unendlichem Band und umgekehrt.Wir wollen den Beweis hier nicht vollständig ausführen, aber die Beweisidee skizzieren. Spannend ist nur die Richtung zu der DTM \(B\) mit einem beidseitig unendlichem Band die äquivalente DTM \(A\) mit einseitig unendlichem Band zu konstruieren.
Beweisidee
Das Band von \(A\) ist einseitig unendlich. Wir können also von einem \(0\)-ten, \(1\)-ten, \(2\)-ten usw. Feld sprechen. Der LSK ist zu Beginn auf dem \(0\)-ten Feld. Das Band von \(B\) ist beidseitig unendlich. Hier wollen wir auch von dem Feld als \(0\)-ten Feld sprechen, auf dem zu Anfang der LSK ist. Rechts davon sind dann das \(1\)-te, \(2\)-te usw. Feld. Links davon wollen wir vom \(-1\)-ten, \(-2\)-ten usw. Feld sprechen.Die Idee ist nun, dass \(A\) sich auf dem \(n\)-ten Feld des Bandes merkt, was auf dem \(n\)-ten \emph{und} dem \(-n\)-ten Feld von \(B\) steht. Dazu ist \(\Gamma \times (\Gamma \cup \{*\})\) das Bandalphabet von \(A\) (\(\Gamma\) ist das Bandalphabet von \(B\)). Man sagt hierzu, dass man das Band in \emph{Spuren} eingeteilt hat. Das Symbol \(*\) wird nur an einer Stelle benötigt, nämlich für das \(0\)-te Feld zudem es keinen negativen Partner gibt. \(A\) merkt sich zusätzlich im Zustand, ob \(B\) gerade im positiven oder negativen Bereich seines Bandes ist. Zustände von \(A\) sind also \([z,P]\) und \([z,N]\) (wobei \(z\) aus \(Z_B\), der Zustandsmenge von \(B\), ist).
\(A\) arbeitet nun wie \(B\) und ändert bei \((x,y) \in \Gamma \times \Gamma\) nur das Element was durch das \(P\) bzw. \(N\) im Zustand vorgegeben wird. Ist man z.B. im Zustand \([z,P]\) und liest \((x,y)\), dann wird geguckt, was \(B\) in \(z\) bei \(x\) machen würde und entsprechend das \(x\) in \((x,y)\) geändert. Der Zustandswechsel und das Bewegen nach links und rechts des LSK ist entsprechend. Nur bei dem \(0\)-ten-Feld muss man aufpassen, da hier ein Wechsel von \(P\) zu \(N\) oder andersherum auftreten kann. Dies ist aber auch einfach durch die \“Uberführungsfunktion von \(A\) abzudecken. Ist man z.B. in \([z,P]\) auf dem Symbol \((x,*)\) und bewegt \(B\) den LSK nach links, so geht man nun in den negativen Bereich des Bandes, d.h. \(A\) wechselt in einen Zustand \([z‘,N]\) und bewegt den LSK nach rechts.
Dies schließt die Konstruktion ab. Es ist dann nicht schwierig zu zeigen, dass tatsächlich [/latex]L(A) = L(B)[/latex] gilt. Hierzu betrachtet man lediglich die Erfolgsrechnungen von \(A\) bzw. von \(B\) und argumentiert, dass dies auch Erfolgsrechnungen in der jeweils anderen Maschine sind, wenn man sich auf das durch \(N\) bzw. \(P\) im Zustand vorgegebene Element von \((x,y)\) beschränkt.
Eine weitere Variante, diesmal aber mit mehr Bändern, ist die \(k\)-Band off-line Turingmaschine. Diese hat neben dem bisherigen Eingabeband, auf dem ja auch gearbeitet wurde, nun \(k\) weitere Arbeitsbänder und ein Ausgabeband. Zudem wird die Nutzung des Eingabebandes und des Ausgabebandes eingeschränkt.
Definiton 4.2.4 (k-Band off-line Turingmaschine)
Eine \(k\)-Band off-line Turingmaschine (kurz \(k\)-Band TM oder auch Mehrband-TM) hat- \(k\) beidseitig unendliche Arbeitsbänder mit jeweils einem eigenen LSK,
- ein Eingabeband, auf dem sie ausschließlich lesen kann, aber den Lese-Kopf dabei in beide Richtungen bewegen darf und
- ein Ausgabeband, auf dem sie nur schreiben und den Schreibkopf ausschließlich von links nach rechts bewegen darf.
Es wären wieder die Definitionen für Konfiguration und Schrittrelation anzupassen, aber wir wollen auch hier darauf verzichten. Ein intuitives Verständnis der Arbeitsweise genügt auch hier. Die \(k\)-Band TM liest stets ein Symbol vom Eingabeband und ein Symbol vom jedem Arbeitsband. Sie kann dann den Kopf auf dem Eingabeband bewegen, mit den Köpfen auf dem Arbeitsband neue Symbole schreiben und diese Köpfe bewegen und sie kann (muss) aber nicht etwas auf das Ausgabeband schreiben, wobei dann der Kopf dort automatisch nach rechts bewegt wird. Diese TM ist sehr praktisch, wenn man von einer TM nur deren Arbeitsweise beschreiben will. Sie ist auch wieder äquivalent zur ursprünglichen DTM.
Satz 4.2.5
Zu jeder \(k\)-Band off-line Turing-Maschine \(A\) mit \(k \geq 1\) gibt es eine äquivalente DTM \(B\) mit nur einem Band und umgekehrt.Wieder ist die Richtung von \(B\) zu \(A\) sofort einsichtig, da man die Fähigkeiten der TM \(A\) quasi nicht nutzt. Man liest einmal die Eingabe vom Band und notiert sie auf einem Arbeitsband. Dort arbeitet man dann so wie mit \(B\) und zuletzt schreibt man ggf. den Bandinhalt noch auf das Ausgabeband. Die Rückrichtung ist interessanter und wir wollen die Beweisidee wieder skizzieren
Beweisidee
Die Idee der Konstruktion ist im Grunde wie eben. Nur teilen wir das Band der \(1\)-Band TM \(B\) nun in mehr als zwei Spuren ein. Wir haben eine Spur für das Eingabeband von \(A\), jeweils eine für jedes Arbeitsband und eine für das Ausgabeband. Da \(A\) außerdem mehr Lese-Schreib-Köpfe hat, muss man für jede Spur markieren, wo der LSK ist, z.B. indem man für jedes Symbol \(x\) noch ein Symbol \(x‘\) einführt, das bedeutet, dass hier der LSK ist. Die \(1\)-Band TM muss dann oft über ihr eines Band wandern, um in jeder Spur die richtige Stelle zu finden und sich dann zu entscheiden, welche Aktion auszuführen ist. Dann muss sie noch mal mehrmals über das Band wandern und jede Stelle aktualisieren.Damit wissen wir, dass deterministische Turingmaschinen mit einem Band, deterministische Turingmaschinen mit \(k\) Arbeitsbändern und deterministische Turingmaschinen mit einem nur einseitig unendlichem Band äquivalent sind. Wir können also je nach Aufgabe eine geeignet erscheinende auswählen. Wir wollen dies hier so machen, dass wir eine Turingmaschine mit einem Band, das in beide Richtungen unendlich ist, nehmen, wenn wir eine TM konstruieren wollen und explizit das Zustandsübergangsdiagramm angeben wollen. Ein Beispiel dafür ist die Turingmaschine für \(L = \{w w^{rev} \mid w \in \{0,1\}^*\}\) aus dem vorherigen Abschnitt.
Mit einer \(k\)-Band off-line TM wollen wir arbeiten, wenn wir nur die Funktionsweise einer TM beschreiben wollen, wenn wir also auf einer gewissen Abstraktionsebene arbeiten wollen. Dies haben wir z.B. bei der Berechnung der Funktion \(f(x) = x – 1\) im vorherigen Abschnitt gemacht. Dort hat allerdings ein Band ausgereicht.
Nutzung von Nichtdeterminismus
Die bisherigen Varianten waren Variationen, die insb. die Nutzung der Bänder betraf, aber weiterhin deterministisch waren. Wie bei DFAs ist es auch bei Turingmaschinen möglich eine nichtdeterministische Variante einzuführen. Hierzu müssen wir nur die \“Uberführungsfunktion anpassen, so dass für ein Tupel \((z,x) \in Z \times \Gamma\) mehrere Folgekonfigurationen möglich sind.
Definiton 4.2.6 (Nichtdeterministische Turingmaschine)
Eine Turingmaschine \(M = (Z, \Sigma, \Gamma, K, z_0, Z_{end})\) heißt nichtdeterministische Turingmaschine (kurz NTM), wenn es zu jedem Paar \((z,x) \in Z \times \Gamma\) eine endliche Anzahl von Übergängen gibt. D.h. es ist $$ K \subseteq Z \times \Gamma \times \Gamma \times \{L, R, H\} \times Z $$ bzw. $$ \delta: Z \times \Gamma \rightarrow 2^{\Gamma \times \{L,R,H\} \times Z} $$ alles andere ist wie bei der DTM definiert.Man könnte wie bei NFAs auch mehrere Startzustände erlauben. Dies ist aber nicht nötig, da eine NTM als erstes nichtdeterministisch in mehrere Folgezustände gehen könnte, ohne den Bandinhalt oder die Position des LSK zu ändern. Wir belassen es daher so, dass die NTM nur einen Startzustand hat.
Die NTM akzeptiert dann ein Eingabewort \(w\) genau dann, wenn es \emph{mindestens eine} Erfolgsrechnung auf \(w\) gibt.
Definiton 4.2.7 (Akzeptierte Sprache einer NTM)
Konfigurationen einer NTM sind wie bei der DTM definiert. Die Konfigurationsübergänge werden so angepasst, dass nicht \(\delta(z,x) = (x‘,B,z‘)\) gelten muss, sondern \((x‘,B,z‘) \in \delta(z,x)\). Darauf aufbauend können dann Rechnung und Erfolgsrechnung und die akzeptierte Sprache analog zu der Definitionen für DTMs definiert werden. Insb. akzeptiert eine NTM genau dann ein Wort \(w\), wenn es von \(z_0 w\) mindestens eine Rechnung gibt, die in eine Konfiguration \(u z_e v\) mit \(z_e \in Z_{end}\) führt.Bei endlichen Automaten haben wir gesehen, dass der Nichtdeterminismus keine entscheidenden Vorteile bringt. Bei Turingmaschinen sieht dies anders aus. Wir betrachten als Beispiel folgendes Problem.
Eingabe: & Ein ungerichteter Graph \(G = (V,E)\) und ein \(k \in \mathbb{N}\).
Frage: & Hat \(G\) eine \(k\)-Clique?
Eine \(k\)-Clique sind dabei \(k\) Knoten des Graphen, die alle paarweise miteinander verbunden sind. Ein Dreieck ist z.B. eine \(3\)-Clique. Wir wollen dieses Problem mit einer Turingmaschine lösen. Die Eingabe für die Turingmaschine ist dabei die Zahl \(k\) gefolgt von einer Liste der Knoten und der Kanten (letzteres als Tupel zweier Knoten).
Mit einer DTM können wir nach und nach alle \(k\)-elementigen Teilmengen von \(V\) durchgehen und prüfen, ob die aktuelle Teilmenge eine \(k\)-Clique ist. Es gibt allerdings recht viele \(k\)-elementigen Teilmengen von \(V\), weswegen dieses Verfahren recht lange dauert. Aber immerhin funktioniert es.

Nach drei Schritten ergibt sich der folgende Konfigurationsbaum, der alle nichtdeterministisch erreichbaren Konfigurationen darstellt. Dieser Baum wird sehr groß.
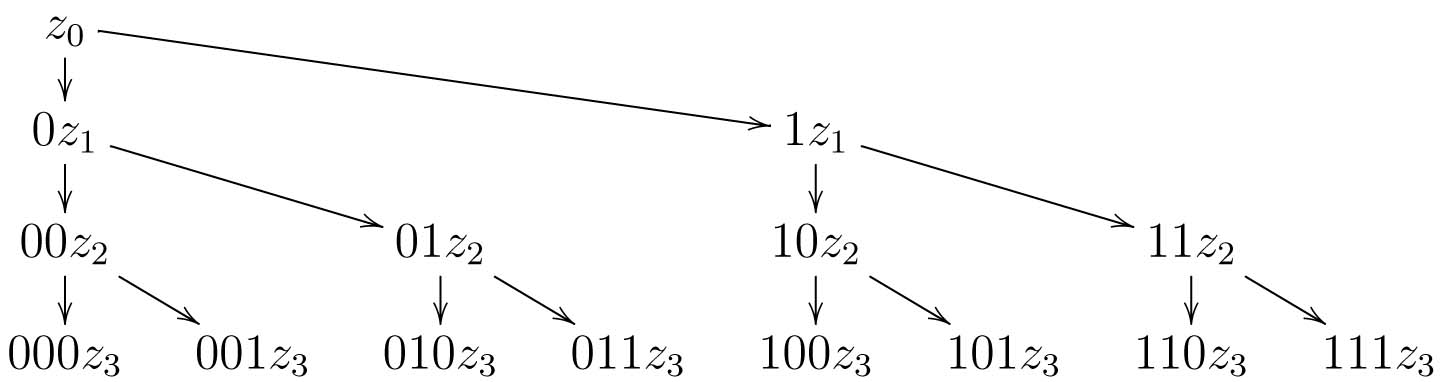
Nun ist die NTM nichtdeterministisch in \(2^{n}\) Konfigurationen. Die Konfigurationen unterscheiden sich dabei nur in der gerade erstellten Bandinschrift des Arbeitsbandes. Auf diesem stehen die Zahlen zwischen \(0^n\) und \(1^n\), was gerade \(2^n\) Zahlen sind. In jeder dieser Konfigurationen geht es jetzt deterministisch weiter, d.h. wir benötigen den Nichtdeterminismus nicht mehr. Im Grunde machen wir nämlich nur das, was wir oben bereits bei der beschriebenen DTM gemacht haben. Von den \(n\) eben geratenen Zahlen bedeutet eine \(1\) an \(i\)-ter Stelle, dass der \(i\)-te Knoten zur Clique gehört (bzw. dass dies geraten wird) und eine \(0\), dass er dies nicht tut. Die NTM überprüft nun zunächst, ob die \(1\) gerade \(k\)-mal vorkommt. Im Anschluss wird überprüft, ob diese \(k\) Knoten tatsächlich eine \(k\)-Clique bilden, d.h. für je zwei davon wird geprüft, ob es eine Kante gibt, die sie verbindet. Falls dies gelingt, wird akzeptiert, sonst nicht. Hat der Graph tatsächlich mindestens eine \(k\)-Clique, so gibt es eine Rechnung der NTM, die diese rät und somit findet. Damit löst die vorgestellt Mehrband-NTM das Problem. Eine Rechnung ist dabei aber viel kürzer als die Rechnung der DTM. Wir kommen auf diesen wichtigen Unterschied später im Rahmen der Komplexitätstheorie zu sprechen.
Wenn man nun die DTM und die NTM für obiges Problem vergleicht, dann ist der Kern bei der NTM, dass diese eine mögliche Lösung nichtdeterministisch rät und dann überprüft, ob diese vermutete Lösung tatsächlich eine ist. Die DTM hingegen kann nur nacheinander alle möglichen Lösungen durchgehen. Man kann an dieser Stelle also fragen, ob eine DTM stets alles kann, was eine NTM kann. Oben können beide das Problem lösen, auch wenn die DTM dies viel langsamer tut. Dennoch erschien die NTM mächtiger. Daher die wichtige Frage:
Tatsächlich sind die beiden Modelle wieder äquivalent. Dabei ist die Richtung von DTM zu NTM wieder klar. Man nutzt den Nichtdeterminismus nicht und kann so ganz einfach eine NTM konstruieren, die die gleiche Sprache akzeptiert wie eine gegebene DTM. Für die Rückrichtung erinnern wir noch einmal an obiges Beispiel einer NTM mit dem zugehörigen Konfigurationsbaum.


Die Idee bei der Konstruktion ist nun, dass es zu jedem Knoten in einem Konfigurationsbaum nur endlich viele Nachfolger geben kann, da die Überführungsfunktion der NTM zwar verschiedene Möglichkeiten anbieten kann, bei einem Zustand, in dem die NTM ist, und Symbol, das sie liest, in eine Nachfolgekonfiguration zu gehen, dies aber stets endlich viele sind. Dieser Konfigurationsbaum kann nun von einer DTM Ebene für Ebene aufgebaut werden und so eine Breitensuche in diesem Baum ausgeführt werden. Tritt dabei eine Konfiguration auf, die einen Endzustand enthält, so wissen wir, dass die NTM akzeptieren würde. In diesem Fall akzeptiert auch die DTM. Ansonsten wird der Baum immer weiter aufgebaut. Wir führen die Idee nachfolgend noch etwas genauer aus.
Satz 4.2.8
Jede von einer NTM akzeptierte Sprache kann auch von einer DTM akzeptiert werden und umgekehrt.Beweisidee
Die Richtung von DTM zu NTM ist klar. Für die Rückrichtung beobachten wir, dass eine Konfiguration \(c_1\) einer NTM, zwar mehrere (nichtdeterministische) Nachfolgekonfiguration haben kann, dass dies aber stets nur endlich viele sind. Seien diese mit \(c_{1,1}, c_{1,2}, \ldots, c_{1,r}\) bezeichnet. Man kann diese Konfigurationen als Baum darstellen mit \(c_1\) als Wurzel und \(c_{1,1}, \ldots, c_{1,r}\) als Kinder von \(c_1\). Die \(c_{1,i}\) haben dann wieder (endlich viele) Kinder \(c_{1,1,1}, \ldots, c_{1,1,j_1}\) und \(c_{1,2,1}, \ldots, c_{1,2,j_2}\) usw., die die dritte Ebene im Baum bilden.Die DTM kann nun die NTM simulieren. Dazu notiert sie auf einem Band (wir konstruieren eine Mehrband-DTM) die Startkonfiguration der NTM. Dann werden alle Nachfolgekonfigurationen dieser Startkonfiguration notiert und die Startkonfiguration gelöscht. Nun wird die erste der eben ermittelten Nachfolgekonfigurationen durch ihre Nachfolgekonfigurationen ersetzt. Dann die zweite der zuerst ermittelten Nachfolgekonfigurationen durch ihre Nachfolgekonfigurationen usw. Auf diese Weise wird der Baum Ebene für Ebene aufgebaut. Wird dabei eine Konfiguration erzeugt, die einen Endzustand enthält, so akzeptiert die DTM.
Wichtig dabei ist, dass nachdem z.B. die Konfiguration \(c_1\) durch ihre Nachfolgekonfigurationen \(c_{1,1}, \ldots, c_{1,r}\) ersetzt wurde, als nächstes mit \(c_2\) weitergemacht wird (nicht mit \(c_{1,1}\)). Auf diese Weise wird erst eine Ebene des Baumes vollständig aufgebaut, bevor in die nächste gegangen wird. So ist sichergestellt, dass man eine Konfiguration mit Endzustand findet, wenn eine existiert. Existiert nämlich eine, so muss es eine in z.B. der \(i\)-ten Ebene des Baumes geben und diese erreicht man. Wandert man anders durch den Baum (macht z.B. oben mit \(c_{1,1}\) weiter, statt mit \(c_2\) und wandert so zunächst in die Tiefe des Baumes), so besteht die Gefahr, dass man Konfigurationen einer unendlich langen Rechnung der NTM erzeugt und nie zu einer anderen Rechnung gelangt, in der vielleicht akzeptiert wird.
So konstruiert, akzeptiert die DTM genau dann, wenn es eine Rechnung der NTM gibt bei der akzeptiert wird und damit also genau dann, wenn die NTM akzeptiert.
Damit haben wir gesehen, dass auch die nichtdeterministische Turingmaschine nicht mächtiger ist als die deterministische. Wie bei NFAs ist es aber oft einfacher eine NTM anzugeben als eine DTM. Außerdem werden wir später sehen, was in diesem Abschnitt schon angedeutet wurde, dass die NTM Probleme scheinbar schneller lösen kann, als eine DTM.
Wir wiederholen die Ergebnisse dieses Abschnittes. Wir haben zunächst verschiedene Varianten der vorher eingeführten deterministischen Turingmaschine eingeführt. Wir haben die deterministische Turingmaschine mit einem einseitig unendlichem Band und eine \(k\)-Band off-line Turingmaschine gesehen und argumentiert, dass diese äquivalent zur deterministischen Turingmaschine mit einem beidseitig unendlichem Band sind. Bei den Beweisen war die Idee, ein Band in Spuren einzuteilen, zentral.
Danach haben wir die nichtdeterministische Turingmaschine eingeführt, die wie der NFA aus einer Konfiguration nichtdeterministisch in verschiedene andere wechseln kann. Wir haben am Beispiel des Clique-Problems gesehen, wie die NTM ein Problem scheinbar deutlich schneller lösen kann, haben aber auch gesehen, dass die DTM dieses Problem, wenn auch scheinbar langsamer, auch lösen kann. Im Anschluss haben wir dann noch gesehen, dass jede NTM von einer DTM simuliert werden kann, die beiden Modelle also auch äquivalent sind. Die Beweisidee war hier, den Konfigurationsbaum der NTM Ebene für Ebene aufzubauen und so eine Breitensuche in diesem Baum mit der DTM zu machen.
