All posts by fgi1
Prädikatenlogik
Zur Prädikatenlogik siehe das zweite Kapitel im Buch Logik für Informatiker von Uwe Schöning.
Semantik
Die Semantik der Aussagenlogik (und die weiteren Themen im Logikteil) finden sich im Buch Logik für Informatiker von Uwe Schöning.
Noch einmal kurz und knapp
Wir fassen den Stoff zur Syntax der Semantik sowie zu den darauf basierenden Themen zur strukturellen Rekursion und zur strukturellen Induktion noch einmal zusammen und wiederholen die einzelnen Begriffe. Bei Unklarheiten zu den einzelnen Begriffen, lohnt sich stets ein Blick in den Haupttext oben.
Wir haben in diesem Abschnitt die Syntax der Aussagenlogik definiert, d.h. wir haben definiert, was wir alles als Formeln der Aussagenlogik bezeichnen wollen. Wichtige Begriffe waren hier: Alphabet, Aussagensymbol, Junktor, atomare Formel, komplexe Formel, wohlgeformte Formel, Formel, Teilformel, Hauptoperator, Negation, Konjunktion, Disjunktion, Implikation und Biimplikation. Als Symbole haben wir \(\neg, \vee, \wedge, \Rightarrow, \Leftrightarrow\) für die Junktoren sowie \(AS_{AL}\) und \(\mathcal{L}_{AL}\) für die Menge der Aussagensymbole bzw. die Menge der wohlgeformten Formeln der Aussagenlogik kennengelernt.
Um die Menge \(\mathcal{L}_{AL}\) zu definieren, haben wir gesagt, dass alle Aussagensymbole (atomare) Formeln sind und dass, wenn \(F\) und \(G\) bereits Formeln sind, dann auch \(\neg F\), \((F \wedge G)\), \((F \vee G)\), \((F \Rightarrow G)\) und \((F \Leftrightarrow G)\) (komplexe) Formeln sind.
Eine wohlgeformte Formel der Aussagenlogik ist dann z.B. die Zeichenkette \(((A \wedge B) \Rightarrow \neg C)\) nicht aber \()A \vee B(\) und zunächst auch z.B. nicht \(A \wedge B\), da wir noch keine Klammerersparnisregeln kennengelernt haben.
Aufbauend auf der Definition der wohlgeformten Formeln der Aussagenlogik haben wir dann mit der strukturellen Rekursion eine Möglichkeit kennengelernt, eine Funktion \(f\) zu definieren, die jeder Formel \(F \in \mathcal{L}_{AL}\) einen Wert \(f(F)\) zuweist.
Um dies auszuführen, um also eine totale Funktion \(f: \mathcal{L}_{AL} \rightarrow D\) zu definieren (wobei \(D\) eine beliebige Menge ist), haben wir gesehen, dass man zunächst in der Rekursionsbasis \(f(A)\) für jedes \(A \in AS_{AL}\) festlegt. Anschließend legt man dann im Rekursionsschritt für die Negation eine Funktion \(f_\neg : D \rightarrow D\) und für jeden zweistelligen Junktor \(\circ \in \{\vee, \wedge, \Rightarrow, \Leftrightarrow\}\) eine Funktion \(f_\circ: D \times D \rightarrow D\) fest. Mit diesen kann dann für eine beliebige Formel \(F\) der Wert \(f(F)\) rekursiv ermittelt werden. Ist bspw. \(F = (G \wedge H)\), so ist \(f(F) = f_\wedge(f(G),f(H))\) und \(f(G)\) und \(f(H)\) müssen rekursiv weiter bestimmt werden.
Als Beispiele für mittels struktureller Rekursion definierte Funktionen haben wir den Grad und die Tiefe einer Formel kennengelernt. Ferner haben wir in einem Exkurs Strukturbäume eingeführt.
Zuletzt haben wir gesehen, wie man, ebenfalls aufbauend auf der Definition der wohlgeformten Formeln der Aussagenlogik, mittels struktureller Induktion die Gültigkeit einer Behauptung für alle Formeln der Aussagenlogik zeigen kann.
Dazu muss man zunächst im Induktionsanfang die Behauptung für alle Aussagensymbole (also alle atomaren Formeln) zeigen. In der Induktionsannahme nimmt man dann an, dass die Behauptung für zwei Formeln \(F\) und \(G\) gilt und zeigt dann im Induktionsschritt, dass die Behauptung (unter dieser Annahme) auch für \(\neg F\), \((F \wedge G)\), \((F \vee G)\), \((F \Rightarrow G)\) und \((F \Leftrightarrow G)\) gilt.
Die strukturelle Induktion ist damit eine (Beweis-)Technik, mit der man Behauptungen für alle Formeln der Aussagenlogik zeigen kann. Exemplarisch haben wir gesehen, dass der Grad einer aussagenlogischen Formeln höchstens so groß werden kann wie die Länge der Formel. Weitere Beispiele sind in den Fragen im Abschnitt zur strukturellen Induktion zu finden.
Strukuturelle Induktion
Im vorherigen Abschnitt haben wir gesehen, wie der Aufbau komplexer Formeln aus einfache(re)n Formeln genutzt werden kann, um Funktionen über die Formelmenge zu definieren. Ähnlich kann man den Aufbau der Formeln nun nutzen, um Eigenschaften von Formeln nachzuweisen. Dies wird als strukturelle Induktion bezeichnet.
Sei für jede Formel \(F \in \mathcal{L}_{AL}\) dazu \(B(F)\) eine Behauptung zu \(F\) (z.B. die Behauptung, dass die Länge von \(F\) stets größer ist als die Anzahl der Operatoren in \(F\)). Wollen wir nun \(B(F)\) für alle Formeln der Aussagenlogik zeigen, so kann dies mittels struktureller Induktion gelingen.
Dazu
1. Zeigt man, dass \(B(F)\) für jede atomare Formel \(F\) gilt (Induktionsanfang).
2. Nimmt man an, dass \(B(F)\) und \(B(G)\) für zwei Formeln \(F\) und \(G\) gelten (Induktionsannahme).
3. Zeigt man, dass unter der Annahme bei 2. nun auch \(B(\neg F), B(F \vee G), B(F \wedge G), B(F \Rightarrow G)\) und \(B(F \Leftrightarrow G)\) gelten (Induktionsschritt).
Wir wollen dies an einem Beispiel illustrieren. Das Beispiel wirkt etwas unnötig, da man die Aussage sofort glaubt, aber es lässt sich gut die Vorgehensweise an diesem Beispiel illustrieren.
Wir wollen zeigen, dass die Anzahl der Junktoren einer Formel begrenzt ist durch die Länge der Formel oder symbolisch: Für jede Formel \(F \in \mathcal{L}_{AL}\) gilt \(grad(F) \leq L(F)\) (dies ist die Behauptung, also obiges \(B(F)\)). Der Grad einer Formel ist im obigen Abschnitt zur strukturellen Rekursion definiert. Die Länge findet sich in dem dortigen Fragen-Abschnitt.
Wir wollen noch kurz darauf eingehen, warum die strukturelle Induktion nützlich ist. An diesem Beispiel lässt sich das nämlich vermutlich nicht so gut erkennen, denn dass die Länge einer Formel stets mindestens so groß ist, wie die Anzahl der Junktoren (die ja auch stets zur Länge beitragen) glaubt man wohl auch ohne Beweis recht schnell. (Man sollte allerdings auch Dinge, die man meint zu sehen, ruhig beweisen. Bisweilen sind sie dann doch nicht so offensichtlich.)
Warum also ist die strukturelle Induktion nützlich? Mit ihr lassen sich quasi nach einem vorgegebenen Schema Behauptungen für alle aussagenlogischen Formeln beweisen. Im Schema muss man zwar noch Lücken füllen (was manchmal recht schwierig ist), aber das Schema gibt einem dennoch eine gute Hilfe. Die strukturelle Induktion ist also quasi ein Beweiswerkzeug oder -schema. Spätere, kompliziertere Behauptungen lassen sich mit ihr gut beweisen. Außerdem lässt sich die strukturelle Induktion auch bei anderen Logiken (oder allgemein bei anderen Strukturen) einführen und ist dort hilfreich. Die strukturelle Induktion dient uns also als Beweisschema und auch wenn wir hier noch keine sinnvollen Beispiele für ihre Anwendung sehen, so gibt es zwei gute Gründe sie hier einzuführen und zu verstehen: 1. Kann sie später für den Beweis komplizierterer Behauptungen genutzt werden und 2. Kann sie später bei anderen Logiken definiert und eingesetzt werden.
Satz 2.3.1
Für jede aussagenlogische Formel \(F\) gilt \(grad(F) \leq L(F)\).Beweis
Wir führen den Beweis mittels struktureller Induktion. Wir gehen zunächst recht ausführlich erklärend vor. Eine kurze Version des Beweises findet sich im Anschluss.
Induktionsanfang. Im Induktionsanfang ist zu zeigen, dass die Aussage für alle atomaren Formeln gilt. Sei also \(A\) ein beliebiges Aussagensymbol (also eine atomare Formel). Da wir \(A\) beliebig wählen, gilt die Behauptung dann, sollten wir sie für \(A\) beweisen können, für alle Aussagensymbole. Betrachten wir nun zuerst was der Grad von \(A\) und die Länge von \(A\) ist, also \(grad(A)\) und \(L(A)\). Nach Definition von \(grad\) ist \(grad(A) = 0\) und nach Definition von \(L\) ist \(L(A) = 1\), womit wir sofort \(grad(A) = 0 \leq 1 = L(A)\) haben. Mit dem Induktionsanfang sind wir nun bereits fertig. Wie eben gezeigt gilt die Aussage für \(A\) und da \(A\) beliebig gewählt war damit für alle Aussagensymbole.
Induktionsannahme. Gelte die Behauptung für zwei Formeln \(F\) und \(G\). So kann man die Induktionsannahme immer schreiben. Es hilft aber oft, sich noch einmal genau zu notieren, was denn nun gilt. Wir schreiben daher: Seien \(F\) und \(G\) Formeln für die die Behauptung gilt, d.h. mit \(grad(F) \leq L(F)\) und \(grad(G) \leq L(G)\).
Induktionsschritt. Wir betrachten nun zunächst \(\neg F\). Wir wollen \(grad(\neg F) \leq L(\neg F)\) zeigen. Betrachten wir zunächst \(grad(\neg F)\) nach Definition von \(grad\) ist \(grad(\neg F) = grad(F) + 1\). Für die Länge gilt nach Definition \(L(\neg F) = L(F) + 1\). Ferner wissen wir aus der Induktionsannahme \(grad(F) \leq L(F)\) (wir haben ja in der Induktionsannahme explizit angenommen, dass \(F\) eine Formel ist mit \(grad(F) \leq L(F)\), daher dürfen wir das jetzt auch benutzen!). Bauen wir dies alles zusammen, so erhalten wir \(grad(\neg F) = grad(F) + 1 \leq L(F) + 1 = L(\neg F)\), wobei die Ungleichung wegen der Induktionsannahme gilt, die beiden Gleichheitszeichen wegen der Definitionen von \(grad\) bzw. \(L\).
Nun betrachten wir \((F \vee G)\). Wir wollen \(grad((F \vee G)) \leq L((F \vee G))\) zeigen. Zunächst ist wegen der Definition von \(grad\) bzw. von \(L\) wieder \(grad((F \vee G)) = grad(F) + grad(G) + 1\) und \(L((F \vee G)) = L(F) + L(G) + 3\). Wegen der Induktionsannahme dürfen wir wieder \(grad(F) \leq L(F)\) und \(grad(G) \leq L(G)\) benutzen. Damit erhalten wir \(grad((F \vee G)) =\) \(grad(F) + grad(G) + 1 \leq\) \(L(F) + L(G) + 1 \leq L(F) + L(G) + 3 =\) \(L((F \vee G))\), wobei die erste \(\leq\)-Beziehung wegen der Induktionsannahme und die zweite einfach wegen \(1 \leq 3\) gilt. Die Gleichheiten gelten wegen der Definitionen von \(grad\) bzw. \(L\).
Die Fälle für \((F \wedge G)\), \((F \Rightarrow G)\) und \((F \Leftrightarrow G)\) zeigt man ganz analog. (Dort passiert tatsächlich überhaupt nichts anderes, da \(grad\) und \(L\) für alle zweistelligen Junktoren gleich definiert sind.)
Vielen, die zum ersten Mal mit der strukturellen Induktion in Berührung kommen, ist nicht klar, warum man die Aussage nun für alle Formeln bewiesen hat? Dies wird nachfolgend erklärt. Wem das klar ist (die Begrüundung ist ganz ähnlich wie bei der vollständigen Induktion), der kann den nachfolgenden Absatz überspringen. Im Anschluss kommt dann noch einmal der Beweis für obige Aussage in deutlich knapperer Form.
Zu Beginn zeigt man im Induktionsanfang die Aussage für alle atomaren Formeln. Für die gilt die Behauptung also schon einmal. Nun nimmt man in der Annahme an, dass \(F\) und \(G\) zwei Formeln sind, für die die Behauptung gilt. Ob es solche Formeln auch gibt, ist eigentlich ganz egal. Man könnte auch weitermachen, wenn es solche nicht gäbe, nur würde man dann nichts sinnvolles beweisen. Es gibt aber bereits Formeln für die wir wissen, dass die Aussage gilt: Die atomaren Formeln nämlich!
Hat man den Induktionsschritt bewiesen, dann weiß man, dass man Formeln für die die Behauptung gilt nun kombinieren kann. Da wir aus dem Induktionsanfang wissen, dass die Behauptung für die atomaren Formeln gilt, gilt sie dann auch für z.B. \((A \wedge B)\). Nun könnte man für das \(F\) aus der Annahme gerade diese Formel nehmen und so auch Schlussfolgern, dass die Behauptung für z.B. \(((A \wedge B) \Rightarrow C)\) gilt. So kann man immer weiter machen und alle Formeln der Aussagenlogik erhalten.
Anders kann man auch sagen, dass man gerade die Definition des Syntax nachbildet. Dort wird nämlich auch gesagt alle Aussagensymbole sind Formeln (für die zeigt man die Behauptung im Induktionsanfang) und dann wird in der Definition der Syntax gesagt wenn \(F\) und \(G\) Formeln sind (vgl. mit der Induktionsannahme!), dann sind auch \(\neg F\), \((F \wedge G)\) usw. Formeln (dies wird durch den Induktionsschritt abgedeckt).
Mit der strukturellen Induktion zeigt man eine Behauptung also tatsächlich für alle Formeln der Aussagenlogik.
Hat man etwas Übung, so geht man bei obigem knapper vor. Zur Illustration wollen wir dies hier einmal machen. Wir wollen \(grad(F) \leq L(F)\) für alle \(F \in \mathcal{L}_{AL}\) beweisen.
Beweis
Wir zeigen dies mittels struktureller Induktion. Der Induktionsanfang ist klar, denn für jedes Aussagensymbol \(A\) gilt \(grad(A) = 0 \leq 1 = L(A)\). Sei nun angenommen, dass \(F\) und \(G\) zwei Formeln sind mit \(grad(F) \leq L(F)\) und \(grad(G) \leq L(G)\). Im Induktionsschritt ergibt sich nun \(grad(\neg F) = grad(F) + 1 \leq L(F) + 1 = L(\neg F)\) und \(grad((F \circ G)) = grad(F) + grad(G) + 1 \leq L(F) + L(G) + 1 \leq L(F) + L(G) + 3 = L((F \circ G))\) für jeden zweistelligen Junktor \(\circ\).
Strukturelle Rekursion
Den in der Definition der Syntax beschriebenen Aufbau komplexer Formeln aus einfache(re)n Formeln kann man nutzen, um Funktionen über die Formelmenge zu definieren und so bspw. eine Funktion \(f\) zu definieren, die jeder Formel \(F\) einen Wert \(f(F)\) zuzuweisen (bspw. die Länge der Formel oder die Anzahl der Junktoren in der Formel). Man nennt dies strukturelle Rekursion).
Ähnlich kann man den Aufbau der Formeln auch nutzen, um Eigenschaften von Formeln nachzuweisen. Dies wird als strukturelle Induktion bezeichnet und wird im nächsten Abschnitt behandelt.
Wenn wir nun mittels struktureller Rekursion eine Funktion definieren wollen, so ist es unser Ziel eine (totale) Funktion \(f: \mathcal{L}_{AL} \rightarrow D\) zu definieren, wobei \(D\) dabei eine beliebige Menge sein kann. \(f\) wird also jeder Formel \(F \in \mathcal{L}_{AL}\) ein Element \(x \in D\) zuweisen. In unserem Fall wird \(D\) meist die Menge \(\mathbb{N}\) der natürlichen Zahlen sein. Um \(f\) nun zu definieren genügt es,
- \(f(A)\) für jedes \(A \in AS_{AL}\) festzulegen und
- eine Funktion \(f_\neg : D \rightarrow D\) und für jeden Junktor \(\circ \in \{\vee, \wedge, \Rightarrow, \Leftrightarrow\}\) eine Funktion \(f_\circ: D \times D \rightarrow D\) zu definieren.
Es ist dann \(f(\neg F) := f_\neg(f(F))\) und z.B. \(f((F \wedge G)) := f_\wedge(f(F), f(G))\) (und analog für die anderen zweistelligen Junktoren).
Die Definition oben erscheint zunächst vielleicht kompliziert. Betrachten wir sie einmal genauer. Zunächst legt man sich auf eine Menge \(D\) fest auf die man abbilden will. Will man z.B. jeder Formel einen Zahlenwert zuweisen? Oder einen Buchstaben? Oder vielleicht eine andere Formel? Wir arbeiten nachfolgend mit Zahlenwerten, also k\"onnen wir ruhig mit \(D = \mathbb{N}\) arbeiten. Zunächst muss dann also für jedes Aussagensymbol \(A \in AS_{AL}\) eine Zahl \(f(A) \in \mathbb{N}\) festgelegt werden (denn \(f\) bildet ja jetzt auf \(D = \mathbb{N}\) ab). Setzen wir einmal \(f(A) = 1\) für jedes \(A \in AS_{AL}\) (man könnte auch verschiedenen Aussagensymbolen verschiedene Werte aus \(\mathbb{N}\) zuweisen, wichtig ist nur, dass jedem Aussagensymbol ein Wert aus \(\mathbb{N}\) zugewiesen wird). Dies wird als Rekursionsbasis bezeichnet.
Im zweiten Schritt wird dann verlangt, dass zunächst eine Funktion \(f_\neg\) definiert wird, die eine natürliche Zahl nimmt und auf eine andere abbildet. Statt dann für z.B. \(\neg A\) und \(\neg B\) explizit \(f(\neg A)\) und \(f(\neg B)\) festzulegen kann man dann die eben festgelegte Rekursionsbasis (die definiert ja u.a. die Werte \(f(A)\) und \(f(B)\)) und die Funktion \(f_\neg\) benutzen und so \(f(\neg A) = f_\neg(f(A))\) bzw. \(f(\neg B) = f_\neg(f(B))\) zu bestimmen. Dies hat neben dem eben genannten Vorteil, dass man deutlich weniger definieren muss, zudem den Vorteil, dass sich die Werte \(f(F)\) für komplexe Formeln \(F\) aus den Werten (unter \(f\)) für Teilformeln von \(F\) ergibt. Ist z.B. \(F\) eine Konjunktion \(F = G \wedge H\), so ermittelt sich \(f(F)\) aus den Werten \(f(G)\) und \(f(H)\), die man dann beide als Argumente von \(f_\wedge\) nutzt. Man bezeichnet die Definition von \(f_\neg\) und der \(f_\circ\) für die zweistelligen Junktoren \(\circ\) als Rekursionsschritt. Man beachte, dass die zweistelligen Junktoren nicht alle gleich behandelt werden müssen.
Zusammenfassend: Will man eine Funktion \(f\) definieren, die jeder Formel \(F\) der Aussagenlogik ein Element aus einer Menge \(D\) zuweist (z.B. einen Zahlenwert aus \(\mathbb{N}\)), so genügt es zunächst \(f\) auf allen atomaren Formeln zu definieren (häufig ist dieser Wert für alle atomaren Formeln gleich). Im Anschluss definiert man dann noch, was passieren soll, wenn man auf einen der Junkotren trifft, d.h. man definiert wie sich der Wert von z.B. \(f(F \wedge G)\) aus den Werten \(f(F)\) und \(f(G)\) ergibt (z.B. k\"onnte man \(f(F \wedge G) = f(F) + f(G) + 3\) setzen, womit man implizit \(f_\wedge(n,m) = n+m+3\) definiert). Unten folgen als Beispiele die Definitionen von Grad und Tiefe. Dort wird (wie meist üblich) in der Rekursionsbasis für alle Aussagensymbole der gleiche Wert genommen und (wie nicht umbedingt üblich aber doch häufig anzutreffen) die Funktionen aller zweistelligen Junktoren stimmen überein.
Damit ist es z.B. möglich den Grad und die Tiefe einer Formel zu definieren.
Definition 2.2.1
Die Funktionen \(grad: \mathcal{L}_{AL} \rightarrow \mathbb{N}\) und \(tiefe: \mathcal{L}_{AL} \rightarrow \mathbb{N}\) werden wie folgt definiert:- Für jedes \(A \in AS_{AL}\) sei
- \(grad(A) = tiefe(A) = 0\).
- Für \(\neg\) sei
- \(grad(\neg F) = grad_\neg(grad(F)) = grad(F) + 1\) und
- \(tiefe(\neg F) = tiefe_\neg(tiefe(F)) = tiefe(F) + 1\).
- (Oder anders: \(grad_\neg : \mathbb{N} \rightarrow \mathbb{N}\) wird definiert durch \(grad_\neg(n) = n + 1\) und entsprechend für \(tiefe_\neg\).
- Für \(\circ \in \{\vee, \wedge, \Rightarrow, \Leftrightarrow\}\) sei
- \(grad((F \circ G)) = grad_\circ(grad(F), grad(G)) = grad(F) + grad(G) + 1\) und
- \(tiefe((F \circ G)) = tiefe_\circ(tiefe(F), tiefe(G)) = max(tiefe(F), tiefe(G)) + 1\).
Für eine Formel \(F\) ist \(grad(F)\) dann der Grad der Formel \(F\) und \(tiefe(F)\) die Tiefe der Formel \(F\).
Informal formuliert ist der Grad einer Formel die Anzahl der Junktoren (bei \(((A \wedge (B \Rightarrow C)) \vee (B \wedge A))\) also \(4\)). Die Tiefe einer Formel ist die Anzahl der Junktoren in der tiefsten Verschachtelung. Führt man noch Strukturbäume ein, so kann man die Tiefe verstehen als die Anzahl der Junktoren auf dem längsten Pfad im Strukturbaum.
Statt Formeln als Zeichenketten der Art \((A \wedge B)\) auszudrücken, kann man Formeln auch als Bäume, sogenannte Strukturbäume, ausdrücken. Dies ist für manche Algorithmen hilfreich.
Ein Strukturbaum zu einer Formel \(F\) ist ein Baum, bei dem die inneren Knoten (die Knoten, die keine Blätter sind) Junktoren sind und die Blätter die atomaren (Teil-)Formeln von \(F\).
Im einzelnen:
- Der Hauptoperator markiert die Wurzel.
- Teilformeln entsprechen Teilbäumen.
- Die Reihenfolge der Teilformeln wird beibehalten (linke Teilformel, linkes Kind).
- Die Aussagesymbole werden dann die Blätter des Baumes.
- Die Junktoren sind die inneren Knoten. Dabei hat \(\neg\) ein Kind, alle anderen Junktoren haben zwei Kinder.
Ein Beispiel veranschaulicht dies schnell. Sei \(F = ((A \vee C) \wedge \neg B)\), dann ergibt sich als Strukturbaum zu \(F\)
Hier ein paar Fragen zur strukturellen Rekursion.
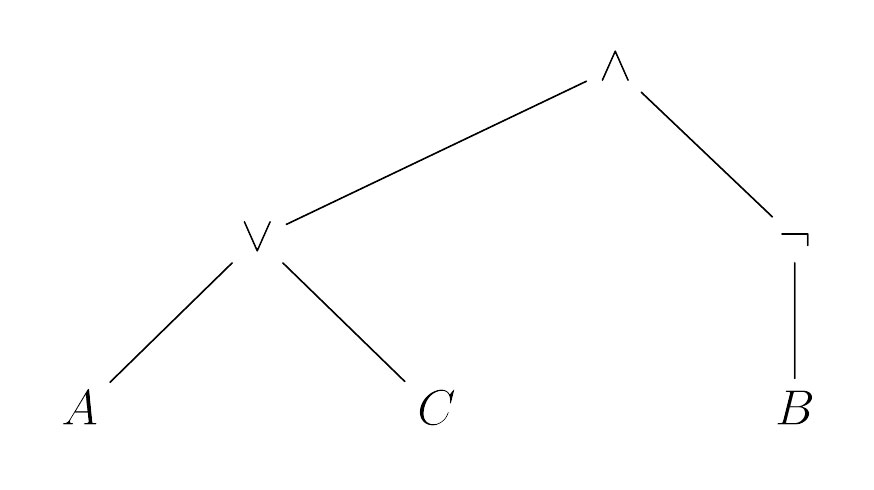
Syntax der Aussagenlogik
Motivation
In den nachfolgenden Abschnitten geht es zunächst um die Syntax und die Semantik der Aussagenlogik. Mit der Syntax definieren wir, was wir überhaupt notieren dürfen. In der Mathematik z.B. ist \(3+4\) ein syntaktisch korrekter Term (man spricht auch von wohlgeformt), die Zeichenkette \(3 ++ 4\) hingegen nicht. Ähnliches wollen wir nun für die Aussagenlogik definieren und damit dann die wohlgeformten Formeln der Aussagenlogik definieren. Dies wird uns dann Notationen wie \(A \wedge B\) erlauben, nicht aber \(\wedge A \wedge B\). Im Anschluss werden wir dann die Semantik definieren. Ziel dabei ist es, jeder Formel einen eindeutigen Wahrheitswert (also eine Bedeutung) zuzuweisen. In der Aussagenlogik kann eine Formel wahr oder falsch ein. Das Ziel ist es ausgehend von Wahrheitswerten für die atomaren Formeln wie \(A\) oder \(B\) und einer Definition für die einzelnen Verknüpfungen, zu einem Wahrheitswert für die ganze Formel (z.B. \(A \wedge B\)) zu kommen.
Aussagenlogische Formeln werden aus einer Menge von Aussagensymbolen (den atomaren Formeln) \(A_1, A_2, A_3, \ldots\) und den Junktoren \(\neg\),\(\wedge\),\(\vee\),\(\Rightarrow\),\(\Leftrightarrow\) (nicht, und, oder, Implikation und Biimplikation) gebildet.
Zunächst ist jedes Aussagensymbol auch eine (atomare) Formel. Ferner kann man, gegeben zwei Formeln \(F\) und\(G\), diese durch die Junktoren zu einer neuen Formel kombinieren. So sind dann auch \(\neg F, (F \wedge G), (F \vee G), (F \Rightarrow G)\) und \((F \Leftrightarrow G)\) (komplexe) Formeln. Damit ist man mit der Definition der Syntax der Aussagenlogik, also damit, wie Formeln „aussehen“ dürfen, auch schon fertig. Eine den obigen Regeln entsprechend gebildete Formel nennt man dann auch wohlgeformt. Wir fassen dies noch einmal in folgender Definition zusammen:
Die Menge der Aussagensymbole ist (abzählbar) unendlich. Dies deutet oben die fortlaufende Indizierung \(A_1, A_2, A_3, \ldots\) an. In jeder Formel treten aber nur endlich viele Aussagensymbole auf. Statt \(A_1\) etc. nimmt man gerne auch Buchstaben am Anfang des Alphabets, also \(A, B, C, \ldots\).
Definition 2.1
Mit \(AS_{AL} = \{A_1, A_2, \ldots\}\) sei die (abzählbar unendliche) Menge der Aussagensymbole der Aussagenlogik bezeichnet.Die Menge \(\mathcal{L}_{AL}\) der (wohlgeformten) Formeln der Aussagenlogik definieren wir mittel
- Jedes \(A \in AS_{AL}\) ist eine (atomare) Formel.
- Ist \(F\) eine Formel, so ist auch\(\neg F\) eine (komplexe) Formel.
- Sind \(F\) und\(G\) Formeln, so sind auch\((F \vee G), (F \wedge G), (F \Rightarrow G)\) und \((F \Leftrightarrow G)\) (komplexe) Formeln.
- Es gibt keine anderen Formeln, als die, die durch endliche Anwendungen der Schritte 1-3 erzeugt werden.
Wir wollen die Definition noch einmal genauer betrachten. Zunächst sind alle Aussagensymbole Formeln. \(A_1\),\(A_2\) usw. sind also Formeln. Dann wird gesagt, wenn \(F\) und \(G\) Formeln sind (und bisher können \(F\) und \(G\) also nur atomare Formeln sein), dann auch z.B. \((F \vee G)\). Sei also z.B. \(F\) die atomare Formel \(A_1\) und \(G\) die atomare Formel \(A_{15}\), dann ist nun \((A_1 \vee A_{15})\) eine Formel. Dies kann man nun weiter fortführen. Nimmt man nun für \(F\) die eben erstellte Formel \((A_1 \vee A_{15})\) und für \(G\) die atomare Formel \(A_6\), so ist z.B. auch \(((A_1 \vee A_{15}) \wedge A_6)\) eine Formel (da im dritten Punkt der Definition oben gesagt wird, wenn \(F\) und \(G\) Formeln sind, dann auch \((F \wedge G))\). Der zweite Punkt der Definition erlaubt noch mit einer Formel \(F\) und dem Symbol \(\neg\) die Formel \(\neg F\) zu konstruieren (also z.B. mit \((A_1 \vee A_{15})\) als \(F\) die Formel \(\neg (A_1 \vee A_{15}))\). Der vierte Punkt sagt dann noch, dass man nur endlich oft so verfahren darf (also keine unendlich langen Formeln entstehen können). Die Definition sagt, dass wir auf diese Weise gerade alle Formeln der Aussagenlogik erhalten.
Nutzen wir die weit verbreitete Konvention, Buchstaben am Anfang des Alphabets für atomare Formeln zu nutzen (also \(A, B, C, \ldots\)), so sind weitere wohlgeformte (d.h. korrekt gebildete) Formeln dann z.B.\(((A \vee B) \Rightarrow C)\) oder \((\neg A \wedge B \wedge \neg C) \vee (A \wedge \neg B \wedge \neg C)\), wobei bei letzterem bereits an mehreren Stellen Klammerersparnisregeln angewandt wurden, d.h. nicht nötige Klammern wurden weggelassen. Dies betraf hier die äusseren Klammern und Klammern, die durch das mehrfache \(\wedge\) aufgetreten wären. Wir kommen später noch auf die Klammerersparnisregeln zu sprechen.
Nicht wohlgeformte Ausdrücke entstehen z.B. durch falsche Klammerung wie in \((F \vee G(\) oder aneinandergereihte Junktoren wie in \(F \vee \vee G\).
In der Mathematik schreibt man ja auch lieber \(3+4+5\) und eher selten \((3+4)+5\) oder gar \(((3+4)+5)\).
Die Syntax definiert also, wie Formeln aussehen dürfen. Darauf aufbauend ist es dann möglich die Semantik zu definieren. Wenn man gar nicht so genau wüsste, wie die Formeln aussehen (sprich: Es nicht wie hier geschehen mit einigen wenigen Konstruktionsvorschriften angeben könnte), könnte man das nämlich nicht machen. Die formale Definition der Syntax wird uns außerdem später in der strukturellen Induktion noch einmal begegnen.
Noch ein paar Begrifflichkeiten. Wir hatten bereits den Begriff des Aussagesymbols und den des Junktors (die \(\neg\), \(\vee\) usw.). Weitere gebräuchliche Begriffe sind Alphabet für die Menge der benutzbaren Symbole. Das Alphabet besteht bei uns also aus den Aussagesymbolen, den Junktoren und den Klammern. Weiterhin nennt man eine Formel, die beim Aufbau einer Formel \(F\) verwendet wird, eine Teilformel von \(F\). Außerdem ist \(F\) Teilformel von sich selbst. Den Junktor, der im letzten Konstruktionsschritt verwendet wurde nennt man den Hauptoperator. Nach dem Hauptoperator werden komplexe Formeln oft benannt. Zum Beispiel ist in der Formel \(F = (A \vee (B \wedge C))\) \((B \wedge C)\) eine Teilformel. Der Hauptoperator ist \(\vee\), weswegen \(F\) auch als Disjunktion bezeichnet wird (im Falle von \(\wedge\) spricht man von einer Konjuktion, bei \(\Rightarrow\) von einer Implikation und bei \(\Leftrightarrow\) von einer Biimplikation).
Hier ein paar Fragen zur Syntax der Aussagenlogik.
Aussagenlogik Einleitung
Die Aussagenlogik ist eine ganz grundlegende Logik, die quasi als Teillogik in den meisten anderen Logiken enthalten ist. So werden z.B. in der Aussagenlogik einfache Verknüpfungen wie nicht, und und oder eingeführt, die man in den meisten anderen Logiken auch haben möchte. Ferner werden in der Aussagenlogik wichtige Konzepte und Begriffe eingeführt, die dann in andere Logiken übernommen werden. Sie ist daher auch hervorragend zum Einüben dieser Konzepte geeignet. Ferner, und für uns besonders interessant, spielt das Erfüllbarkeitsproblem der Aussagenlogik, d.h. die Frage, gegeben eine Formel der Aussagenlogik, kann diese zu wahr ausgewertet werden, eine zentrale Rolle in der Komplexitätstheorie und wird uns dort wieder begegnen.
Wir werden zunächst die Syntax der Aussagenlogik einführen, d.h. wir werden formal einführen, wie die Formeln der Aussagenlogik eigentlich aussehen dürfen, was wir also hinschreiben dürfen. Im Anschluss werden wir die Semantik der Aussagenlogik einführen, d.h. wir werden definieren, wann eine Formel wahr und wann eine Formel falsch ist und wie wir zu diesen Werten kommen. Nachfolgend geht es dann um Beziehungen zwischen Formeln. Hier führen wir die Begriffe der Folgerbarkeit und der Äquivalenz ein. Es wird dann viel darum gehen Formeln auf diese Eigenschaft zu prüfen und darauf, ob sie wahr gemacht werden können. Wir werden sehen, dass dies zwar gemacht werden kann, aber mit den nahe liegenden Verfahren zu aufwändig ist. Daher werden wir uns noch mit weiteren Verfahren wie z.B. der Resolution beschäftigen.
Motivation Logik
Im Logikteil wollen wir zwei Logiken, die Aussagenlogik und die Prädikatenlogik, betrachten. Logiken spielen in der Informatik bei den verschiedensten Anwendungen eine wichtige Rolle. Mit ihr lassen sich Sachverhalte aus der realen Welt abstrakt ausdrücken (es wird also quasi ein Modell der Welt in der Logik ausgedrückt). In der Logik können dann Schlussfolgerungen gezogen werden und diese können dann wieder als Sachverhalte in der realen Welt interpretiert werden. Ein Grundbaustein der Logik sind die Formeln. Beispielsweise ist \(N \vee \neg R\) eine aussagenlogische Formel, die für „ich bin nass (\(N\)) oder (\(\vee\)) es regnet (\(R\)) nicht (\(\neg\))“ stehen könnte. Wenn man nun wüsste das dieser Sachverhalt und zusätzlich noch \(R\) (es regnet) gilt, könnte man schlussfolgern, dass dann \(N\) gelten muss (ich bin nass). Mit der Logik können wir solche Schlussfolgerungen formalisieren, sie in komplizierteren Kontexten machen und dies auch (in Teilen) automatisieren.
Die Einsatzgebiete der verschiedenen Logiken sind in der Informatik recht vielfältig. So finden sie z.B. Einsatz bei dem Thema künstliche Intelligenz, bei Datenbanken, bei der Beschreibung von technischen Schaltkreisen, in der Software- und Hardwareverifikation, als Grundlage von logikorientierten Programmiersprachen wie beispielsweise Prolog und noch in etlichen Bereichen mehr. In vielen dieser Bereiche ist zudem ein Zusammenspiel von Logik und Automaten von Bedeutung. So werden z.B. in der Verifikation oft die System durch Automaten modelliert und durch eine Formel in einer Logik eine bestimmte Eigenschaft spezifiziert. Die Frage ist dann, ob das Modell die Spezifikation erfüllt. Wir werden nur am Rande und nicht vertiefend auf diese Anwendungsgebiete der Logik eingehen können. In späteren, vertiefenden Veranstaltungen wird einem die Logik aber immer wieder begegnen, so dass ein gutes Grundlagenwissen hierzu sehr nützlich ist.
Oftmals werden in verschiedenen Anwendungs- und Forschungskontexten verschiedene oder spezielle Logiken eingesetzt. Wir behandeln nachfolgend die Aussagenlogik und die Prädikatenlogik.
NP-Vollständigkeit
Für die erwähnten Probleme aus \(NP\) des vorherigen Abschnittes wie z.B. das Mengenpartitionsproblem sind keine deterministischen Algorithmen in Polynomialzeit bekannt. Wir würden dies nun gerne zeigen können, d.h. wir würden gerne zeigen können, dass sich das Problem für kein \(k\) in \(O(n^k)\) lösen lässt. Leider fehlen uns hierfür trotz intensiver Forschung die nötigen Techniken. Wir verfolgen daher einen anderen Ansatz. Wir zeigen für ein Problem \(X\) (von dem wir vermuten, dass es nicht in \(P\) ist), dass es bestimmte Eigenschaften hat, so dass, sollte \(X\) doch in \(P\) liegen, sehr unwahrscheinliche Dinge folgen würden.
Reduktionen
Um unser oben beschriebenes Ziel zu erreichen, wollen wir von einem Problem sagen können, dass es zu den schwierigsten Problemen seiner Klasse gehört. Hierzu brauchen wir den Begriff der Reduktion.
Definiton 5.3.1 (Reduktion)
Seien \(L_1, L_2 \subseteq \{0,1\}^*\) zwei Sprachen. Wir sagen, dass \(L_1\) auf \(L_2\) \emph{in polynomialer Zeit reduziert wird}, wenn eine in Polynomialzeit berechenbare Funktion \(f : \{0,1\}^* \rightarrow \{0,1\}^*\) existiert mit$$ x \in L_1 \text{ genau dann wenn } f(x) \in L_2 $$
für alle \(x \in \{0,1\}^*\).
Hierfür schreiben wir dann \(L_1 \leq_p L_2\). \(f\) wird als Reduktionsfunktion, ein Algorithmus, der \(f\) berechnet, als Reduktionsalgorithmus bezeichnet.
Andere Symbole für die Reduktion sind \(L_1 \leq_{pol} L_2\) oder auch \(L_1 \leq^p_m L_2\). Das \(m\) steht dabei für „many-one“, da man zwei (oder mehr) \(x,y \in L_1\) auf das gleiche \(f(x) = f(y) = u \in L_2\) abbilden darf. (Ebenso darf man zwei (oder mehr) \(x‘,y‘ \not\in L_1\) auf das gleiche \(f(x‘) = f(y‘) = u‘ \not\in L_2\) abbilden.)
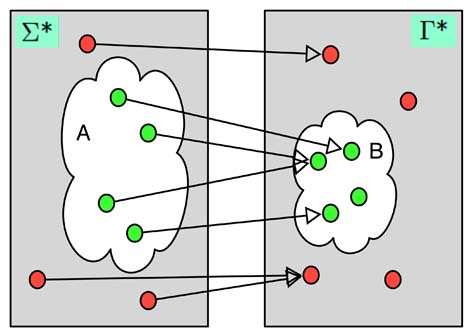
Allgemeiner kann man eine Reduktion zu zwei Sprachen \(A \subseteq \Sigma^*\) und \(B \subseteq \Gamma^*\) als eine Funktion \(f: \Sigma^* \rightarrow \Gamma^*\) mit \(x \in A\) gdw. \(f(x) \in B\) für alle \(x \in \Sigma^*\) definieren. Den Sprachen können also verschiedene Alphabete zugrunde liegen und die Reduktion muss (zunächst) nicht in Polynomialzeit möglich sein. Man kann dann unterschiedliche Zeitreduktionen einführen und so z.B. auch \(P\)-vollständige Probleme definieren (was dann die schwierigsten Probleme in \(P\) sind).
Hat man eine Reduktion \(f: \{0,1\}^* \rightarrow \{0,1\}^*\) von \(L_1\) auf \(L_2\), so ist das wichtige, dass jedes \(x \in L_1\) (man spricht hier auch von Ja-Instanzen, da dies ein \(x\) ist, bei dem eine Turingmaschine für \(L_1\) (sofern eine existiert) mit ja antworten würde) auf ein \(y \in L_2\) abgebildet wird, also auf eine Ja-Instanz von \(L_2\). Ja-Instanzen werden also auf Ja-Instanzen und Nein-Instanzen auf Nein-Instanzen abgebildet. Die Fragen „Ist \(x \in L_1\)?“ und „Ist \(f(x) \in L_2\)?“ haben also stets die gleiche Antwort. Dies werden wir gleich ausnutzen. Die Abbildung verdeutlicht noch einmal eine Reduktion. Wir haben hier den allgemeinen Fall zweier Sprachen \(A \subseteq \Sigma^*\) und \(B \subseteq \Gamma^*\) skizziert. Man beachte, dass Ja-Instanzen auf Ja-Instanzen und Nein-Instanzen auf Nein-Instanzen abgebildet werden und dass mehrere Ja-Instanzen auf eine Ja-Instanz abgebildet werden können (und genauso mehrere Nein-Instanzen auf eine Nein-Instanz).
Man beachte, dass Ja-Instanzen auf Ja-Instanzen und Nein-Instanzen auf Nein-Instanzen abgebildet werden und dass mehrere Ja-Instanzen auf eine Ja-Instanz abgebildet werden können (und genauso mehrere Nein-Instanzen auf eine Nein-Instanz). Da Ja-Instanzen auf Ja-Instanzen abgebildet werden und Nein-Instanzen auf Nein-Instanzen und da die Reduktion per Definition berechenbar ist lassen sich Reduktionen ausnutzen, um Probleme durch andere zu lösen. Die Kernidee dabei ist, erst die Reduktion zu benutzen und dann das Problem, auf das reduziert wurde, zu lösen (und damit dann auch das ursprüngliche). Der folgende Satz konkretisiert dies.
Satz 5.3.2
Seien \(L_1, L_2 \subseteq \{0,1\}^*\) mit \(L_1 \leq_p L_2\), dann folgt aus \(L_2 \in P\) auch \(L_1 \in P\).Beweise
Wir wissen aus den Voraussetzungen zunächst, dass wegen \(L_1 \leq_p L_2\) eine in Polynomialzeit berechenbare Reduktionsfunktion \(f\) existiert mit \(x \in L_1\) genau dann, wenn \(f(x) \in L_2\). Ferner gibt es wegen \(L_2 \in P\) einen Algorithmus \(A_2\), der \(L_2\) in Polynomialzeit entscheidet.Wir müssen damit zeigen, dass es einen Algorithmus \(A_1\) gibt, der \(L_1\) in Polynomialzeit entscheidet. Die Idee ist zunächst die Reduktion zu berechnen und dann \(A_2\) zu benutzen. Im einzelnen arbeitet \(A_1\) auf einer Eingabe \(x \in \{0,1\}^*\) wie folgt:
- Berechne \(f(x)\).
- Nutze \(A_2\), um \(f(x) \in L_2\) zu entscheiden.
- Antworte genau so wie \(A_2\).
Da \(f\) berechenbar ist, klappt der erste Schritt. Da \(A_2\) ebenfalls ein Algorithmus ist, der stets terminiert, klappt auch der zweite Schritt. Und zuletzt produziert der dritte Schritt wegen \(f(x) \in L_2\) gdw. \(x \in L_1\) gerade die richtige Antwort.
Wir sind damit fast feritg. Wir müssen noch zeigen, dass \(A_1\) auch in Polynomialzeit arbeitet (bisher haben wir nur gezeigt, dass er die korrekten Ergebnisse liefert). Die richtige Laufzeit sieht man so ein: Zunächst kann \(f\) in Polynomialzeit berechnet werden. Daher ist die Länge des Wortes, das bei der Reduktion berechnet wird (also die Länge von \(f(x)\)), polynomiell in \(x\) beschränkt, d.h. es ist \(|f(x)| \in O(|x|^c)\) (mit einer Konstanten \(c\)). Die Eingabe von \(A_2\) ist \(f(x)\), daher ist zur Berechnung der Laufzeit von \(A_2\) dann \(|f(x)|\) relevant. Die Laufzeit von \(A_2\) ist durch \(O(|f(x)|^d) = O(|x|^{c \cdot d})\) beschränkt, wobei \(d\) wieder eine Konstante ist. Damit ist eine obere Schranke für die Laufzeit von \(A_1\) dann \(O(|x|^c + |x|^{c \cdot d}) = O(|x|^{c \cdot d})\) und somit läuft \(A_1\) in Polynomialzeit und es ist \(L_1 \in P\).
Der obige Satz erlaubt es ein Problem (das \(L_1\) in obigem Satz) durch ein anderes (das \(L_2\)) zu lösen. Darum auch die Benennung Reduktion. Statt einen Algorithmus für \(L_1\) zu finden und so \(L_1\) zu lösen, nutzt man einen für \(L_2\) und löst so nicht nur \(L_2\), sondern (dank des Reduktionsalgorithmus) auch \(L_1\). Das Problem, \(L_1\) zu lösen, ist also darauf „reduziert“worden, das Problem \(L_2\) zu lösen. Man beachte aber, dass ein Reduktionsalgorithmus auch nichts anderes ist als ein ganz normaler Algorithmus. Die Aufgabe eines Reduktionsalgorithmus ist es aber, eine Probleminstanz in eine andere umzuwandeln. Also z.B. eine Instanz eines Graphenproblems in eine Instanz eines zahlentheoretischen Problems. (Man kann daher eine Reduktion auch als Transformation bezeichnen.)
Wenn wir nun für zwei Probleme \(A\) und \(B\) zeigen, dass \(A \leq_p B\) gilt, so wissen wir, dass \(A\) höchstens so schwierig wie \(B\) ist (höchstens bezieht sich hier auf den polynomiellen Mehraufwand, der hier (im Falle von Problemen in \(P\) und \(NP\)) als akzeptabel angsehen wird). \(A\) kann nämlich nicht schwieriger sein, denn sonst löst man \(A\) einfach indem man erst die Reduktion benutzt und dann \(B\) löst. Daher auch die Notation mit dem Kleiner-Gleich-Zeichen. Reduziert man nun jede Sprache aus \(NP\) auf eine (neue) Sprache \(L\), so ist \(L\) mindestens so schwierig wie ganz \(NP\), denn löst man nun \(L\), so kann man (mittels des Umwegs über die Reduktion) nun jedes Problem aus \(NP\) lösen. Das macht dann \(L \in NP\) sehr unwahrscheinlich, denn dann würde \(P = NP\) gelten, was als sehr unwahrscheinlich angesehen wird, da sich Generationen von Wissenschaftlern mit den verschiedenen Problemen in \(NP\) beschäftigt haben und nie für irgendeines dieser Probleme auf einen Algorithmus in \(P\) gekommen sind. – Es gibt noch weitere gute Gründe, warum \(P = NP\) unwahrscheinlich ist, diese führen hier aber etwas zu weit. Wir merken uns an dieser Stelle, dass es gute Gründe gibt \(P \not= NP\) anzunehmen. Bewiesen ist dies aber nicht!
Wir wollen nun obiges mit dem Begriff der \(NP\)-Vollständigkeit formalisieren und dann an Beispielen illustrieren, wie uns dies helfen kann für Probleme zumindest zu zeigen, dass es unter der Annahme \(P \not= NP\) keinen Algorithmus in Polynomialzeit geben kann. Da die Annahme ein recht starkes Fundament hat, ist dies dann schon eine recht starke Aussage.
Definition der \(NP\)-Vollständigkeit
Wir führen den wichtigen Begriff der \(NP\)-Vollständigkeit ein, der in der theoretischen Informatik und der Algorithmik eine fundamentale Bedeutung hat.
Definiton 5.3.3
Eine Sprache \(L \subseteq \{0,1\}^*\) wird als \(NP\)-vollständig bezeichnet, wenn- \(L \in NP\) und
- \(L‘ \leq_p L\) für jedes \(L‘ \in NP\) gilt.
Kann man für \(L\) zunächst nur die zweite Eigenschaft beweisen, so ist \(L\) \(NP\)-schwierig (-schwer/-hart).
Alle \(NP\)-vollständigen Probleme bilden die Komplexitätsklasse \(NPC\).
Da wir dies nun formal definiert haben, können wir den folgenden wichtigen Satz beweisen:
Satz 5.3.4
Sei \(L \in NPC\). Ist nun \(L \in P\), so ist \(NP = P\).Beweis
Wir erinnern an den Satz aus dem letzten Abschnitt: Sind \(L_1, L_2 \subseteq \{0,1\}^*\) mit \(L_1 \leq_p L_2\), dann folgt aus [/latex]L_2 \in P[/latex] auch \(L_1 \in P\).Sei hier nun \(L \in NPC\) und \(L \in P\) also \(L \in NPC \cap P\). Wir wollen \(P = NP\) zeigen. Dabei ist \(P \subseteq NP\) klar. Zu zeigen ist also noch \(NP \subseteq P\). Sei dazu nun \(L‘ \in NP\). Wegen \(L \in NPC\) gilt \(L‘ \leq_p L\) und aus \(L \in P\) folgt mit dem oben wiederholten Satz aus dem letzten Abschnitt \(L‘ \in P\) und wir sind bereits fertig.
Eine äquivalente Formulierung des Satzes von eben ist: Gibt es ein \(L \in NP \setminus P\), so ist \(NPC \cap P = \emptyset\). Es ist eine gute Übung sich zu überlegen, warum dies gilt.
Der letzte Satz rechtfertigt nun gerade die Aussage, dass ein Problem in \(NPC\) (also ein \(NP\)-vollständiges Problem) höchstwahrscheinlich nicht effizient lösbar ist (also in \(P\) ist). Dann würde nämlich \(P = NP\) gelten und damit wären alle Probleme in \(NP\) (darunter auch all die komplizierten aus \(NPC\)) effizient lösbar (in \(P\)), was aller Erfahrung widersprechen würde.
Wir betonen noch einmal, dass es sehr gute Gründe gibt, \(P \not= NP\) anzunehmen und dass es daher eine sehr starke Aussage ist, wenn man sagt, dass ein bestimmter Sachverhalt nur gilt, wenn \(P = NP\) ist. Der Sachverhalt kann dann praktisch ausgeschlossen werden. Trotzdem ist es nicht sicher, dass \(P = NP\) gilt. Man ist sich in dieser Hinsicht allerdings so sicher, dass teilweise Sicherheitsprotokolle auf dieser Annahme basieren.
Unser Ziel ist es nun Probleme als \(NP\)-Vollständig nachweisen zu können. Wir könnten dann immer versuchen einen schnellen Algorithmus für ein neues Problem zu finden und, sollte dies nicht klappen, versuchen zu zeigen, dass das Problem \(NP\)-vollständig ist. Gelingt letzteres, können wir im Allgemeinen aufhören zu versuchen einen schnellen Algorithmus zu finden (und können beginnen andere Ansätze zu verfolgen, z.B. Algorithmen entwickeln, die nur eine fast optimale Lösung liefern und ähnliches). Um dies zu erreichen, zeigen wir zunächst noch zwei weitere wichtige Sätze (mit den obigen sind es dann drei wichtige). Der erste Satz sagt uns etwas über die Transitivität von \(\leq_p\), was man auch interpretieren kann als eine Hintereinanderausführung von Reduktionsalgorithmen. Der zweite Satz sagt uns darauf aufbauend etwas darüber, wie Probleme als \(NP\)-vollständig nachgewiesen werden können.
Satz 5.3.5
Ist \(L_1 \leq_p L_2\) und \(L_2 \leq_p L_3\), so ist \(L_1 \leq_p L_3\).Beweis
Das Argument ist ähnlich wie bei dem Beweis, dass \(L_1 \in P\) aus \(L_1 \leq_p L_2\) und \(L_2 \in P\) folgt. Seien \(f\) und \(g\) die Reduktionsfunktionen aus \(L_1 \leq_p L_2\) bzw. \(L_2 \leq_p L_3\). Bei Eingabe \(x\) mit \(|x| = n\) berechnen wir zunächst \(f(x)\) in Polynomialzeit \(p(n)\). Dann berechnen wir \(g(f(x))\) in Zeit \(q(|f(x)|) \leq q(p(n))\). Insgesamt ist der Aufwand dann bei Eingaben der Länge \(n\) durch \(p(n) + q(p(n))\) nach oben beschränkt, was ein Polynom ist. (Die Eigenschaft \(x \in L_1\) gdw. \((g \circ f)(x) \in L_3\) folgt direkt aus den gegebenen Reduktionen. Die hier gesuchte Reduktionsfunktion ist also \(g \circ f\).)Satz 5.3.6
Sei \(L\) eine Sprache und \(L‘ \in NPC\). Gilt \(L‘ \leq_p L\), so ist \(L\) \(NP\)-schwierig. Ist zusätzlich \(L \in NP\), so ist \(L\) \(NP\)-vollständig.Beweis
Wegen \(L‘ \in NPC\) gilt \(L“ \leq_p L‘\) für jedes \(L“ \in NP\). Aus \(L‘ \leq_p L\) und dem vorherigen Satz folgt dann \(L“ \leq_p L\), \(L\) ist also \(NP\)-schwierig. Ist zusätzlich \(L \in NP\), so ist \(L\) nach Definition \(NP\)-vollständig.Aus dem letzten Satz lässt sich ein Verfahren ableiten, wie vorgegangen werden kann, wenn man von einem neuen Problem \(L\) zeigen will, dass es \(NP\)-vollständig ist.
- Zeige \(L \in NP\).
- Wähle ein \(L‘ \in NPC\) aus.
- Gib einen Algorithmus an, der ein \(f\) berechnet, das jede Instanz
\(x \in \{0,1\}^*\) von \(L‘\) auf eine Instanz \(f(x)\) von \(L\) abbildet (also eine Reduktion). - Beweise, dass \(f\) die Eigenschaft \(x \in L‘\) gdw. \(f(x) \in L\)
für jedes \(x \in \{0,1\}^*\) besitzt. - Beweise, dass \(f\) in Polynomialzeit berechnet werden kann.
Hierbei zeigen die letzten drei Punkte \(L‘ \leq_p L\). Mit dem letzten Satz folgt daraus und aus den ersten beiden Punkten dann \(L \in NPC\).
Das Problem ist nun, dass, um im zweiten Schritt des Verfahrens ein \(L‘ \in NPC\) auswählen zu können, man erstmal welche haben muss! Je mehr man hier kennt, desto besser ist es später, aber ein erstes brauchen wir und dort werden wir tatsächlich alle Probleme aus \(NP\) auf dieses reduzieren müssen! (Denn für das erste Problem können wir obiges Verfahren noch nicht anwenden, da der zweite Schritt nicht möglich ist.)
Als erstes \(NP\)-vollständige Problem nehmen wir das auch historisch erste \(NP\)-vollständige Problem nämlich das Erfüllbarkeitsproblem der Aussagenlogik \(\texttt{SAT}\) (für Satisfiability).
Definiton 5.3.7 (SAT)
Das Erfüllbarkeitsproblem der Aussagenlogik ist definiert als das Entscheidungsproblem \(\texttt{SAT}\) mit$$ \texttt{SAT} = \{\langle \phi \rangle \mid \phi \text{ ist eine erfüllbare aussagenlogische Formel}\} $$
Satz 5.3.7
\(\texttt{SAT}\) ist \(NP\)-vollständig.Beweis
Um \(\texttt{SAT} \in NP\) zu zeigen, raten wir gegeben eine Formel \(\phi\) eine Belegung (es gibt \(2^n\) viele bei \(n\) verschiedenen Variablen in \(\phi\)) und verifizieren in Polynomialzeit, ob sie die Formel erfüllt.Um zu zeigen, dass \(\texttt{SAT}\) vollständig ist für \(NP\) müssen wir alle Probleme aus \(NP\) auf \(\texttt{SAT}\) reduzieren. Die Beweisidee ist zu einer Sprache \(L \in NP\) die Turingmaschine \(M\) mit \(L(M) = L\) zu betrachten und alle Kopfbewegungen und damit mögliche Konfigurationsübergänge in einer Formel zu kodieren. Ist diese Formel erfüllbar, gibt es eine akzeptierende Rechnung, sonst nicht. Die genaue Konstruktion ist interessant, führt hier aber zu weit. Man findet den Beweis z.B. im Buch von Hopcroft, Ullman und Motwani.
Hat man nun erstmal ein \(NP\)-vollständiges Problem, so kann man (dem Plan oben entsprechend) nun dieses benutzen, um weitere Probleme als \(NP\)-vollständig nachzuweisen. Der umständliche Weg \emph{alle} \(NP\)-Probleme auf ein neues zu reduzieren entfällt so (bzw. man kriegt dies insb. wegen der Transitivität von \(\leq_p\) geschenkt). Je größer dann der Vorrat an \(NP\)-vollständigen Problemen ist, desto größer ist die Auswahl an Problemen, von denen man eine Reduktion auf ein neues Problem, dessen Komplexität noch unbekannt ist, versuchen kann. (Es gibt natürlich immer die Möglichkeit alle Probleme aus \(NP\) auf ein neues zu reduzieren, aber i.A. wird dies nicht gemacht, sondern wie im Verfahren oben beschrieben vorgegangen.)
Wir wollen neben \(\texttt{SAT}\) noch zwei weitere Probleme als \(NP\)-vollständig voraussetzen. Die Beweise finden sich wieder im Buch von Hopcroft, Ullman und Motwani.
Satz 5.3.9
Die Probleme$$ \texttt{CNF} = \{\langle \phi \rangle \mid \phi \text{ ist eine erfüllbare aussagenlogische Formel in KNF}\} $$
und
$$ \texttt{3CNF} = \{\langle \phi \rangle \mid \phi \in CNF, \text{jede Klausel hat genau drei verschiedene Literale}\} $$
sind \(NP\)-vollständig.
Beweis
\(\texttt{CNF}, \texttt{3CNF} \in NP\) ist klar. Man kann dann \(\texttt{SAT} \leq_p \texttt{CNF}\) und \(\texttt{CNF} \leq_p \texttt{3CNF}\) zeigen (siehe wieder das Buch von Hopcroft, Ullman und Motwani).Neben den eben betrachten \(\texttt{Clique}-\) und \(\texttt{Big-Clique}\)-Problem sind auch die anderen im letzten Abschnitt eingeführten \(NP\)-Probleme, das Mengenpartitonsproblem, das Teilsummenproblem und das Färbungsproblem alle \(NP\)-vollständig. Daneben gibt es noch tausende weitere und für keines dieser Probleme ist ein effizienter Algorithmus (d.h. ein Algorithmus, der in Polynomialzeit läuft) bekannt. Dies bestärkt uns in dem Glauben, dass ein Nachweis von \(L \in NPC\) bedeutet, dass \(L\) nicht in \(P\) liegt. Denn wäre es in \(P\), würden all die tausenden von Probleme, für die kein effizienter Algorithmus gefunden werden konnte, plötzlich in \(P\) sein.
Daher kann man nun, gegeben ein Problem für das man einen Algorithmus entwickeln will, dies zunächst versuchen. Fallen einem aber nach einiger Zeit und etlichem Nachdenken stets nur Algorithmen ein, die \emph{im Prinzip den ganzen Suchraum durchgehen}, so ist das Problem vermutlich \(NP\)-vollständig (oder schlimmer). Dies kann man dann versuchen nachzuweisen. Gelingt dies, kann man die Suche nach einem effizienten Algorithmus zugunsten von anderen Ansätzen verwerfen. Möglichkeiten diese Probleme dennoch zu attackieren sind z.B. Einschränkungen der Eingabe zu betrachten (vielleicht braucht man ja nur mit Bäumen zu arbeiten statt mit allgemeinen Graphen), Approximationsalgorithmen zu entwickeln (mit denen man i.A. nicht das Optimum ermittelt, aber vielleicht einen Wert, der gut genug ist), randomisierte Algorithmen zu entwickeln (die manchmal kein Ergebnis liefern) oder Heuristiken zu entwickeln (bei denen sowohl die Laufzeit als auch die Güte des Ergebnisses meist unklar sind). Diese Möglichkeiten sind Inhalt von weiterführenden Veranstaltungen zur Algorithmik.
Hier ein paar Fragen zur NP-Vollständigkeit.