Bisher haben wir mit Turingmaschinen so wie mit den bisherigen Automatenmodellen Sprachen akzeptiert. Eingangs haben wir aber gesagt, dass die Turingmaschine insbesondere als Modell für das Berechenbare dienen soll. Tatsächlich kann man mit Turingmaschinen auch Funktionen berechnen. Dies ist auch gar nicht so überraschend, denn wenn wir z.B. zwei Zahlen addieren wollen, dann können wir diese Zahlen ja bspw. binär kodieren, was zwei Worte über dem Alphabet \(\{0,1\}\) ergibt. Das Ergebnis kann ebenfalls binär kodiert werden, so dass die DTM dann eine Wortfunktion \(\Sigma^* \rightarrow \Sigma^*\) berechnet mit z.B. \(\Sigma = \{0,1,\$\}\), wobei das Dollarzeichen als Trennsymbol zwischen den beiden Eingabeargumenten dient. Kurz gesagt ist es wenig überraschend, dass die TM Funktionen berechnen kann, weil wir die Argumente einer Funktion ebenso wie das Bild kodieren können, ganz so wie wir Menschen das ja auch machen, indem wir das Symbol \(3\) für die Zahl \(3\) nehmen.
Will man dies genau definieren, so muss man festlegen, wie die DTM startet und wie sie enden soll, wenn sie eine Funktion berechnet. Wir definieren dies wie folgt.
Definiton 4.1.5 (Turing-berechenbare Funktionen)
Sei \(\Sigma\) ein Alphabet und \(f: \Sigma^* \rightarrow \Sigma^*\) eine (möglicherweise partielle) (Wort-)Funktion. \(f\) heißt Turing-berechenbar oder kürzer berechenbar oder auch partiell rekursiv genau dann, wenn es eine DTM \(A\) gibt mit: $$ z_0 w \vdash^* z_e v \text{ für ein \(z_e \in Z_{end}\) gdw. } f(w) = v $$Wir verlangen also, dass die DTM in \(z_0 w\) startet und in \(z_e v\) endet, wenn \(f(w) = v\) ist und andersherum. Ist \(f\) auf einem Wert \(w‘\) nicht definiert, so wird auch nicht gesagt, was die TM tut. Sie sollte nur nicht in einer Konfiguration \(z_e v\) enden, da das ja \(f(w‘) = v\) impliziert. Sinnvollerweise macht man das so, dass die DTM in einem solchen Fall in einen Zustand geht, der einen Fehler signalisiert.
Man kann das Berechnen von Funktionen noch explizit für Funktionen definieren, die mit natürlichen Zahlen arbeiten.
Definiton 4.1.6
Eine (partielle) Funktion \(f: \mathbb{N}^r \rightarrow \mathbb{N}^s\) heißt (Turing-)berechenbar oder partiell rekursiv genau dann, wenn es eine DTM gibt mit$$ z_0 0^{m_1+1} 1 0^{m_2 + 1} 1 \ldots 1 0^{m_r+1} \vdash^*
z_e 0^{n_1+1} 1 0^{n_2 + 1} 1 \ldots 1 0^{n_s+1} $$
$$genau~dann,~wenn$$
$$ f(m_1, m_2, \ldots, m_r) = (n_1, n_2, \ldots, n_s) $$
und der Funktionswert definiert ist.
Die DTM arbeitet in diesem Fall also mit dem Alphabet \(\{0,1\}\) und kodiert die einzelnen Argumente von \(f\) unnär, d.h. eine Zahl wie z.B. \(4\) wird durch vier \(0\)en kodiert. Hier genauer sogar durch vier plus eine, damit man die Zahl \(0\) mit einer \(0\) ausdrücken kann, die Zahl \(1\) dann mit zweien usw.
Häufig braucht man obiges aber gar nicht, sondern arbeitet mit Wortfunktionen wie in der ersten Definition. Hat man eine Funktion, die mit natürlichen Zahlen arbeitet, dann kodiert man die Zahlen i.A. ohnehin binär und nicht unnär. Man kann dann wie eingangs erwähnt mit einem Alphabet wie \(\{0,1,\$\}\) arbeiten. Eine DTM würde dann z.B. bei der Additionsfunktion für \(f(9,4) = 13\) mit der Eingabe \(1001\$100\) beginnen und \(1101\) berechnen, also gerade die Zahlen in Binärkodierung, nur dass dies dann je nach Sichtweise Binärzahlen oder eben Worte über dem Alphabet \(\{0,1\}\) sind.
Als Beispiel wollen wir eine DTM beschreiben, die die Funktion \(f(x) = x-1\) berechnet. Dabei sei \(x\) eine natürliche Zahl, die in Binärkodierung gegeben ist. Wir wollen also eine DTM beschreiben, die die Wortfunktion von \(x\) nach \(f(x)\) berechnen.
Die DTM beginnt in der Konfiguration \(z_0 x\) und arbeitet wie folgt:
- Fahre zum am weitesten rechts stehenden Zeichen von \(x\).
- Ist dies eine \(1\), schreibe eine \(0\) und fahre bei Schritt \(4\) fort.
- Ist dies eine \(0\), schreibe eine \(1\), gehe ein Feld nach links und mach bei Schritt \(2\) weiter.
- Fahre ganz nach links und gehe in einen Endzustand.
Die DTM setzt gerade das schriftliche subtrahieren von \(1\) um. Man beachte noch, dass im letzten Schritt ganz nach links gefahren wird, so dass wir in einer Konfiguration \(z_e y\) enden, wobei \(y = x + 1\) ist (bzw. Worte, die dies ausdrücken) und \(z_e\) ein Endzustand ist.
Aus obiger Beschreibung lässt sich leicht das Zustandsübergangsdiagramm einer DTM gewinnen. Man muss lediglich auf Dinge achten, wie dass man im ersten Schritt über alle Symbole rüber liest, bis man auf ein \(\#\) trifft, dann geht man mit dem LSK wieder nach links und ist nun auf dem letzten Symbol von \(x\). Entsprechendes passiert bei dem letzten Schritt. Hier ist es dann nützlich, dass das Band in \emph{beide} Richtungen unendlich ist.
Funktionen wie \(f(x) = x+y\) kann man ähnlich berechnen. Eine DTM könnte zunächst von \(x\) das am weitesten rechts stehende Symbol lesen, dann von \(y\) und sich beides im Zustand merken. Weiter rechts wird dann das Ergebnis aufgebaut. Dann werden die nächsten Symbole von \(x\) und \(y\) gelesen und das Ergebnis weiter aufgebaut. Im Zustand kann man sich zudem einen eventuellen \"Ubertrag merken. Zum Schluss muss man dann, um der Definition zu entsprechen, noch das Band so aufräumen, dass \(x\) und \(y\) gelöscht sind, nur das Ergebnis auf dem Band steht und der LSK ganz links von diesem steht.
Im Grunde genommen ist das Arbeiten mit einer DTM also wie das Arbeiten mit einer (sehr) eingeschränkten Programmiersprache.
Als zweites Beispiel wollen wir eine kompliziertere Funktion berechnen. Wir wollen eine DTM konstruieren, die die Funktion \(f(w) = w^{rev}\) für \(w \in \{0,1\}^*\) berechnet, also eine DTM, die ein Eingabewort umdreht. Als Mensch würde man das Wort von hinten anfangen zu lesen und dann von rechts nach links lesen und das Gelesene Symbol für Symbol woanders von links nach rechts aufbauen. Genau diese Idee können wir auch in eine Turingmaschine kodieren.
Die DTM setzt folgende Idee bei Eingabe eines Wortes \(w\) um:
- Marker \(\$\) sowohl links als auch rechts vom Wort \(w\) setzen.
- Lese letztes Symbol von \(w\) und ersetze es durch \(\#\).
- Wandere nach rechts über das \(\$\) herüber und speichern das Symbol dort. (Im Zustand merken, welches Symbol zu schreiben ist.)
- Wiederhole dies, d.h. lösche das Wort \(w\) von rechts nach links, Buchstabe für Buchstabe und baue das Wort \(w^{rev}\) rechts davon und von links nach rechts Buchstabe für Buchstabe auf.
- Zu Beachten:
- bei \(w\) muss über die schon gelöschten Buchstaben (d.h. über die \(\#\)) rüber gelesen werden; bei \(w^{rev}\) muss über das schon geschriebene Teilwort herübergelesen werden.
- \(w\) wurde zu Ende gelesen, wenn man auf das zweite \(\$\) trifft.
- Lösche die beiden \(\$\) und bewege den Kopf an den Anfang von \(w^{rev}\).
Die schon recht komplizierte DTM ist nachfolgend abgebildet.
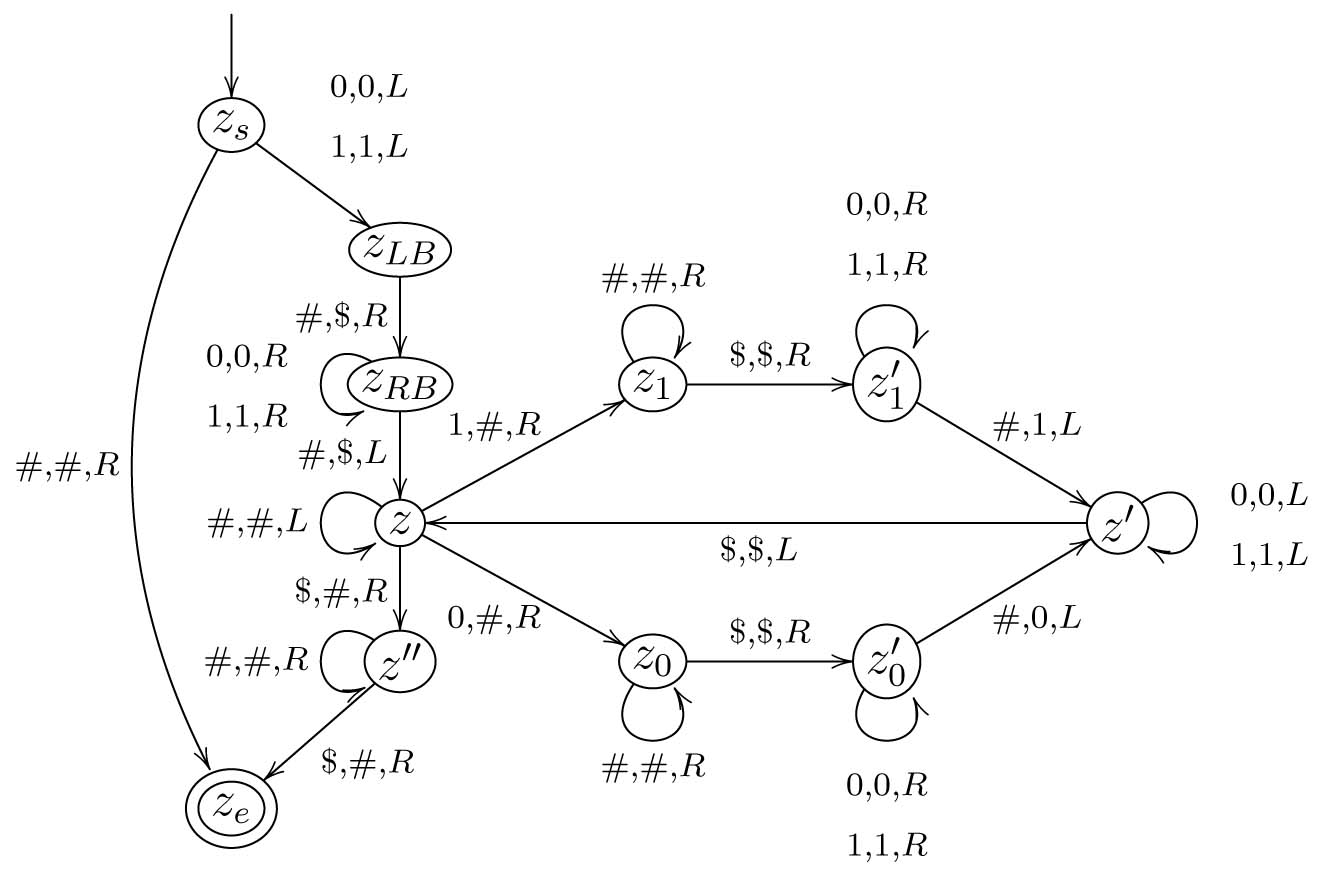
Man beachte, wie sich die in der Idee beschriebene Schleife in der DTM im Kreis \(z, z_1, z_1', z'\) bzw. \(z, z_0, z_0', z'\) wieder findet.
Es ist nun noch genauer zu begründen, dass tatsächlich \(z_s w \vdash^* z_e w^{rev}\) genau dann, wenn \(f(w) = w^{rev}\) gilt. Da \(f\) total ist, genügt es zu zeigen, dass die Turingmaschine in \(z_s w\) gestartet, stets in der Konfiguration \(z_e w^{rev}\) endet. Dazu genügt es an dieser Stelle die Arbeitsweise detailliert zu beschreiben. Wir werden dabei nämlich merken, dass die DTM nie blockiert und stets aus \(w\) das Spiegelwort macht, wie gewünscht. Wir beachten zuerst, dass der Sonderfall des leeren Wortes durch die Kante von \(z_s\) nach \(z_e\) abgedeckt ist. Hat \(w\) also mindestens die Länge \(1\), dann arbeitet die Turingmaschine wie folgt. Zunächst macht sie einen Schritt nach links und setzt in \(z_{LB}\) die linke Begrenzung. Dann geht sie in \(z_{RB}\) über \(w\) herüber und setzt die rechte Begrenzung. In \(z\) angekommen ist die Konfiguration nun also stets \(\$vzx\$\) mit \(vx = w\). Der LSK ist also über dem letzten Symbol von \(w\). Nun verfährt die DTM wie folgt. Das letzte noch nicht gelöschte Symbol von \(w\) wird von rechts gesucht (daher die Schleife an \(z\)). Wird eine \(1\) gefunden, so wird nach \(z_1\) gegangen, bei einer \(0\) nach \(z_0\). Hier wird nun in \(z_1\) (bzw. \(z_0\)) über die schon gelöschten Symbole von \(w\) gelesen, bis der Grenzmarker \(\$\) gefunden wird. In \(z_1'\) bzw. \(z_0'\) wird über das schon konstruierte Teilwort von \(w^{rev}\) gelesen bis das Ende gefunden wird. Hier wird dann eine \(1\) bzw. \(0\) angefügt und nach \(z'\) gewechselt. Man beachte, dass das \(i\)-te Symbol von \emph{rechts} von \(w\) an die \(i\)-te Stelle von \emph{links} vom bisher aufgebauten Teilwort gesetzt wird. Daher wird hier genau \(w^{rev}\) konstruiert. In \(z'\) wird nun wieder über das bereits konstruierte Teilwort von \(w^{rev}\) gelesen, dann der Wechsel nach \(z\) gemacht und dort wieder über das bereits gelöschte Teilwort von \(w\) gelesen. Dies wird in einer Schleife wiederholt bis irgendwann \(w\) komplett gelöscht ist. Dies wird dadurch bemerkt, dass in \(z\) der erste Grenzmarker (das links von \(w\) positionierte \(\$\)) gefunden wird. Dieser wird dann gelöscht und nach \(z''\) gewechselt, wo der andere Grenzmarker gesucht wird und ebenfalls gelöscht wird. Die DTM gelangt so stets in die Konfiguration \(z_e w^{rev}\), was den Beweis abschliesst, da die TM nur genau so und nicht anders arbeiten kann, also stets bei jedem Wort \(w\) genau das Wort \(w^{rev}\) konstruiert und in der Konfiguration \(z_e w^{rev}\) endet.
Wir wollen abschließend noch darauf eingehen, dass, obwohl unterschiedlich definiert, das Akzeptieren von Sprachen und das Berechnen von Funktionen sehr ähnlich sind. Akzeptiert eine Turingmaschine eine Sprache \(L\), so tut sie im Grunde nichts anderes als die charakteristische Funktion von \(L\) zu berechnen.
Berechnet eine Turingmaschine andersherum eine Funktion \(f: M \rightarrow N\), so kann man leicht eine Turingmaschine konstruieren, die die Sprache \(L = \{ (x, f(x)) \mid x \in M \}\) akzeptieren soll (hierzu müssen ggf. \(M\) und \(N\) geeignet kodiert werden).
Nehmen wir einmal \(f(x,y) = x+y\) als Beispiel. Eine Turingmaschine, die diese Funktion berechnet, würde in einer Konfiguration \(z_0 x \$ y\) starten und in einer Konfiguration \(z_e f(x,y)\) enden. Will man lieber über das Akzeptieren von Sprachen sprechen, was uns insbesondere in der Komplexitätstheorie nützen wird, so betrachtet man stattdessen die Sprache \(L = \{ (x,y,z) \mid x+y = z \}\). Hat man bereits eine Turingmaschine, die \(f\) berechnet, lässt sich leicht eine konstruieren, die \(L\) akzeptiert. Die neue Turingmaschine benutzt die alte als Subprogramm, um \(x+y\) zu berechnen und vergleicht das Ergebnis mit \(z\). Sie akzeptiert genau dann, wenn dieser Vergleich positiv ist.
