Für die erwähnten Probleme aus \(NP\) des vorherigen Abschnittes wie z.B. das Mengenpartitionsproblem sind keine deterministischen Algorithmen in Polynomialzeit bekannt. Wir würden dies nun gerne zeigen können, d.h. wir würden gerne zeigen können, dass sich das Problem für kein \(k\) in \(O(n^k)\) lösen lässt. Leider fehlen uns hierfür trotz intensiver Forschung die nötigen Techniken. Wir verfolgen daher einen anderen Ansatz. Wir zeigen für ein Problem \(X\) (von dem wir vermuten, dass es nicht in \(P\) ist), dass es bestimmte Eigenschaften hat, so dass, sollte \(X\) doch in \(P\) liegen, sehr unwahrscheinliche Dinge folgen würden.
Reduktionen
Um unser oben beschriebenes Ziel zu erreichen, wollen wir von einem Problem sagen können, dass es zu den schwierigsten Problemen seiner Klasse gehört. Hierzu brauchen wir den Begriff der Reduktion.
Definiton 5.3.1 (Reduktion)
Seien \(L_1, L_2 \subseteq \{0,1\}^*\) zwei Sprachen. Wir sagen, dass \(L_1\) auf \(L_2\) \emph{in polynomialer Zeit reduziert wird}, wenn eine in Polynomialzeit berechenbare Funktion \(f : \{0,1\}^* \rightarrow \{0,1\}^*\) existiert mit$$ x \in L_1 \text{ genau dann wenn } f(x) \in L_2 $$
für alle \(x \in \{0,1\}^*\).
Hierfür schreiben wir dann \(L_1 \leq_p L_2\). \(f\) wird als Reduktionsfunktion, ein Algorithmus, der \(f\) berechnet, als Reduktionsalgorithmus bezeichnet.
Andere Symbole für die Reduktion sind \(L_1 \leq_{pol} L_2\) oder auch \(L_1 \leq^p_m L_2\). Das \(m\) steht dabei für „many-one“, da man zwei (oder mehr) \(x,y \in L_1\) auf das gleiche \(f(x) = f(y) = u \in L_2\) abbilden darf. (Ebenso darf man zwei (oder mehr) \(x‘,y‘ \not\in L_1\) auf das gleiche \(f(x‘) = f(y‘) = u‘ \not\in L_2\) abbilden.)
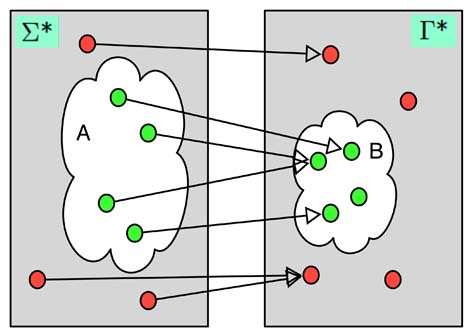
Allgemeiner kann man eine Reduktion zu zwei Sprachen \(A \subseteq \Sigma^*\) und \(B \subseteq \Gamma^*\) als eine Funktion \(f: \Sigma^* \rightarrow \Gamma^*\) mit \(x \in A\) gdw. \(f(x) \in B\) für alle \(x \in \Sigma^*\) definieren. Den Sprachen können also verschiedene Alphabete zugrunde liegen und die Reduktion muss (zunächst) nicht in Polynomialzeit möglich sein. Man kann dann unterschiedliche Zeitreduktionen einführen und so z.B. auch \(P\)-vollständige Probleme definieren (was dann die schwierigsten Probleme in \(P\) sind).
Hat man eine Reduktion \(f: \{0,1\}^* \rightarrow \{0,1\}^*\) von \(L_1\) auf \(L_2\), so ist das wichtige, dass jedes \(x \in L_1\) (man spricht hier auch von Ja-Instanzen, da dies ein \(x\) ist, bei dem eine Turingmaschine für \(L_1\) (sofern eine existiert) mit ja antworten würde) auf ein \(y \in L_2\) abgebildet wird, also auf eine Ja-Instanz von \(L_2\). Ja-Instanzen werden also auf Ja-Instanzen und Nein-Instanzen auf Nein-Instanzen abgebildet. Die Fragen „Ist \(x \in L_1\)?“ und „Ist \(f(x) \in L_2\)?“ haben also stets die gleiche Antwort. Dies werden wir gleich ausnutzen. Die Abbildung verdeutlicht noch einmal eine Reduktion. Wir haben hier den allgemeinen Fall zweier Sprachen \(A \subseteq \Sigma^*\) und \(B \subseteq \Gamma^*\) skizziert. Man beachte, dass Ja-Instanzen auf Ja-Instanzen und Nein-Instanzen auf Nein-Instanzen abgebildet werden und dass mehrere Ja-Instanzen auf eine Ja-Instanz abgebildet werden können (und genauso mehrere Nein-Instanzen auf eine Nein-Instanz).
Satz 5.3.2
Seien \(L_1, L_2 \subseteq \{0,1\}^*\) mit \(L_1 \leq_p L_2\), dann folgt aus \(L_2 \in P\) auch \(L_1 \in P\).Beweise
Wir wissen aus den Voraussetzungen zunächst, dass wegen \(L_1 \leq_p L_2\) eine in Polynomialzeit berechenbare Reduktionsfunktion \(f\) existiert mit \(x \in L_1\) genau dann, wenn \(f(x) \in L_2\). Ferner gibt es wegen \(L_2 \in P\) einen Algorithmus \(A_2\), der \(L_2\) in Polynomialzeit entscheidet.Wir müssen damit zeigen, dass es einen Algorithmus \(A_1\) gibt, der \(L_1\) in Polynomialzeit entscheidet. Die Idee ist zunächst die Reduktion zu berechnen und dann \(A_2\) zu benutzen. Im einzelnen arbeitet \(A_1\) auf einer Eingabe \(x \in \{0,1\}^*\) wie folgt:
- Berechne \(f(x)\).
- Nutze \(A_2\), um \(f(x) \in L_2\) zu entscheiden.
- Antworte genau so wie \(A_2\).
Da \(f\) berechenbar ist, klappt der erste Schritt. Da \(A_2\) ebenfalls ein Algorithmus ist, der stets terminiert, klappt auch der zweite Schritt. Und zuletzt produziert der dritte Schritt wegen \(f(x) \in L_2\) gdw. \(x \in L_1\) gerade die richtige Antwort.
Wir sind damit fast feritg. Wir müssen noch zeigen, dass \(A_1\) auch in Polynomialzeit arbeitet (bisher haben wir nur gezeigt, dass er die korrekten Ergebnisse liefert). Die richtige Laufzeit sieht man so ein: Zunächst kann \(f\) in Polynomialzeit berechnet werden. Daher ist die Länge des Wortes, das bei der Reduktion berechnet wird (also die Länge von \(f(x)\)), polynomiell in \(x\) beschränkt, d.h. es ist \(|f(x)| \in O(|x|^c)\) (mit einer Konstanten \(c\)). Die Eingabe von \(A_2\) ist \(f(x)\), daher ist zur Berechnung der Laufzeit von \(A_2\) dann \(|f(x)|\) relevant. Die Laufzeit von \(A_2\) ist durch \(O(|f(x)|^d) = O(|x|^{c \cdot d})\) beschränkt, wobei \(d\) wieder eine Konstante ist. Damit ist eine obere Schranke für die Laufzeit von \(A_1\) dann \(O(|x|^c + |x|^{c \cdot d}) = O(|x|^{c \cdot d})\) und somit läuft \(A_1\) in Polynomialzeit und es ist \(L_1 \in P\).
Der obige Satz erlaubt es ein Problem (das \(L_1\) in obigem Satz) durch ein anderes (das \(L_2\)) zu lösen. Darum auch die Benennung Reduktion. Statt einen Algorithmus für \(L_1\) zu finden und so \(L_1\) zu lösen, nutzt man einen für \(L_2\) und löst so nicht nur \(L_2\), sondern (dank des Reduktionsalgorithmus) auch \(L_1\). Das Problem, \(L_1\) zu lösen, ist also darauf „reduziert“worden, das Problem \(L_2\) zu lösen. Man beachte aber, dass ein Reduktionsalgorithmus auch nichts anderes ist als ein ganz normaler Algorithmus. Die Aufgabe eines Reduktionsalgorithmus ist es aber, eine Probleminstanz in eine andere umzuwandeln. Also z.B. eine Instanz eines Graphenproblems in eine Instanz eines zahlentheoretischen Problems. (Man kann daher eine Reduktion auch als Transformation bezeichnen.)
Wenn wir nun für zwei Probleme \(A\) und \(B\) zeigen, dass \(A \leq_p B\) gilt, so wissen wir, dass \(A\) höchstens so schwierig wie \(B\) ist (höchstens bezieht sich hier auf den polynomiellen Mehraufwand, der hier (im Falle von Problemen in \(P\) und \(NP\)) als akzeptabel angsehen wird). \(A\) kann nämlich nicht schwieriger sein, denn sonst löst man \(A\) einfach indem man erst die Reduktion benutzt und dann \(B\) löst. Daher auch die Notation mit dem Kleiner-Gleich-Zeichen. Reduziert man nun jede Sprache aus \(NP\) auf eine (neue) Sprache \(L\), so ist \(L\) mindestens so schwierig wie ganz \(NP\), denn löst man nun \(L\), so kann man (mittels des Umwegs über die Reduktion) nun jedes Problem aus \(NP\) lösen. Das macht dann \(L \in NP\) sehr unwahrscheinlich, denn dann würde \(P = NP\) gelten, was als sehr unwahrscheinlich angesehen wird, da sich Generationen von Wissenschaftlern mit den verschiedenen Problemen in \(NP\) beschäftigt haben und nie für irgendeines dieser Probleme auf einen Algorithmus in \(P\) gekommen sind. – Es gibt noch weitere gute Gründe, warum \(P = NP\) unwahrscheinlich ist, diese führen hier aber etwas zu weit. Wir merken uns an dieser Stelle, dass es gute Gründe gibt \(P \not= NP\) anzunehmen. Bewiesen ist dies aber nicht!
Wir wollen nun obiges mit dem Begriff der \(NP\)-Vollständigkeit formalisieren und dann an Beispielen illustrieren, wie uns dies helfen kann für Probleme zumindest zu zeigen, dass es unter der Annahme \(P \not= NP\) keinen Algorithmus in Polynomialzeit geben kann. Da die Annahme ein recht starkes Fundament hat, ist dies dann schon eine recht starke Aussage.
Definition der \(NP\)-Vollständigkeit
Wir führen den wichtigen Begriff der \(NP\)-Vollständigkeit ein, der in der theoretischen Informatik und der Algorithmik eine fundamentale Bedeutung hat.
Definiton 5.3.3
Eine Sprache \(L \subseteq \{0,1\}^*\) wird als \(NP\)-vollständig bezeichnet, wenn- \(L \in NP\) und
- \(L‘ \leq_p L\) für jedes \(L‘ \in NP\) gilt.
Kann man für \(L\) zunächst nur die zweite Eigenschaft beweisen, so ist \(L\) \(NP\)-schwierig (-schwer/-hart).
Alle \(NP\)-vollständigen Probleme bilden die Komplexitätsklasse \(NPC\).
Da wir dies nun formal definiert haben, können wir den folgenden wichtigen Satz beweisen:
Satz 5.3.4
Sei \(L \in NPC\). Ist nun \(L \in P\), so ist \(NP = P\).Beweis
Wir erinnern an den Satz aus dem letzten Abschnitt: Sind \(L_1, L_2 \subseteq \{0,1\}^*\) mit \(L_1 \leq_p L_2\), dann folgt aus [/latex]L_2 \in P[/latex] auch \(L_1 \in P\).Sei hier nun \(L \in NPC\) und \(L \in P\) also \(L \in NPC \cap P\). Wir wollen \(P = NP\) zeigen. Dabei ist \(P \subseteq NP\) klar. Zu zeigen ist also noch \(NP \subseteq P\). Sei dazu nun \(L‘ \in NP\). Wegen \(L \in NPC\) gilt \(L‘ \leq_p L\) und aus \(L \in P\) folgt mit dem oben wiederholten Satz aus dem letzten Abschnitt \(L‘ \in P\) und wir sind bereits fertig.
Eine äquivalente Formulierung des Satzes von eben ist: Gibt es ein \(L \in NP \setminus P\), so ist \(NPC \cap P = \emptyset\). Es ist eine gute Übung sich zu überlegen, warum dies gilt.
Der letzte Satz rechtfertigt nun gerade die Aussage, dass ein Problem in \(NPC\) (also ein \(NP\)-vollständiges Problem) höchstwahrscheinlich nicht effizient lösbar ist (also in \(P\) ist). Dann würde nämlich \(P = NP\) gelten und damit wären alle Probleme in \(NP\) (darunter auch all die komplizierten aus \(NPC\)) effizient lösbar (in \(P\)), was aller Erfahrung widersprechen würde.
Wir betonen noch einmal, dass es sehr gute Gründe gibt, \(P \not= NP\) anzunehmen und dass es daher eine sehr starke Aussage ist, wenn man sagt, dass ein bestimmter Sachverhalt nur gilt, wenn \(P = NP\) ist. Der Sachverhalt kann dann praktisch ausgeschlossen werden. Trotzdem ist es nicht sicher, dass \(P = NP\) gilt. Man ist sich in dieser Hinsicht allerdings so sicher, dass teilweise Sicherheitsprotokolle auf dieser Annahme basieren.
Unser Ziel ist es nun Probleme als \(NP\)-Vollständig nachweisen zu können. Wir könnten dann immer versuchen einen schnellen Algorithmus für ein neues Problem zu finden und, sollte dies nicht klappen, versuchen zu zeigen, dass das Problem \(NP\)-vollständig ist. Gelingt letzteres, können wir im Allgemeinen aufhören zu versuchen einen schnellen Algorithmus zu finden (und können beginnen andere Ansätze zu verfolgen, z.B. Algorithmen entwickeln, die nur eine fast optimale Lösung liefern und ähnliches). Um dies zu erreichen, zeigen wir zunächst noch zwei weitere wichtige Sätze (mit den obigen sind es dann drei wichtige). Der erste Satz sagt uns etwas über die Transitivität von \(\leq_p\), was man auch interpretieren kann als eine Hintereinanderausführung von Reduktionsalgorithmen. Der zweite Satz sagt uns darauf aufbauend etwas darüber, wie Probleme als \(NP\)-vollständig nachgewiesen werden können.
Satz 5.3.5
Ist \(L_1 \leq_p L_2\) und \(L_2 \leq_p L_3\), so ist \(L_1 \leq_p L_3\).Beweis
Das Argument ist ähnlich wie bei dem Beweis, dass \(L_1 \in P\) aus \(L_1 \leq_p L_2\) und \(L_2 \in P\) folgt. Seien \(f\) und \(g\) die Reduktionsfunktionen aus \(L_1 \leq_p L_2\) bzw. \(L_2 \leq_p L_3\). Bei Eingabe \(x\) mit \(|x| = n\) berechnen wir zunächst \(f(x)\) in Polynomialzeit \(p(n)\). Dann berechnen wir \(g(f(x))\) in Zeit \(q(|f(x)|) \leq q(p(n))\). Insgesamt ist der Aufwand dann bei Eingaben der Länge \(n\) durch \(p(n) + q(p(n))\) nach oben beschränkt, was ein Polynom ist. (Die Eigenschaft \(x \in L_1\) gdw. \((g \circ f)(x) \in L_3\) folgt direkt aus den gegebenen Reduktionen. Die hier gesuchte Reduktionsfunktion ist also \(g \circ f\).)Satz 5.3.6
Sei \(L\) eine Sprache und \(L‘ \in NPC\). Gilt \(L‘ \leq_p L\), so ist \(L\) \(NP\)-schwierig. Ist zusätzlich \(L \in NP\), so ist \(L\) \(NP\)-vollständig.Beweis
Wegen \(L‘ \in NPC\) gilt \(L“ \leq_p L‘\) für jedes \(L“ \in NP\). Aus \(L‘ \leq_p L\) und dem vorherigen Satz folgt dann \(L“ \leq_p L\), \(L\) ist also \(NP\)-schwierig. Ist zusätzlich \(L \in NP\), so ist \(L\) nach Definition \(NP\)-vollständig.Aus dem letzten Satz lässt sich ein Verfahren ableiten, wie vorgegangen werden kann, wenn man von einem neuen Problem \(L\) zeigen will, dass es \(NP\)-vollständig ist.
- Zeige \(L \in NP\).
- Wähle ein \(L‘ \in NPC\) aus.
- Gib einen Algorithmus an, der ein \(f\) berechnet, das jede Instanz
\(x \in \{0,1\}^*\) von \(L‘\) auf eine Instanz \(f(x)\) von \(L\) abbildet (also eine Reduktion). - Beweise, dass \(f\) die Eigenschaft \(x \in L‘\) gdw. \(f(x) \in L\)
für jedes \(x \in \{0,1\}^*\) besitzt. - Beweise, dass \(f\) in Polynomialzeit berechnet werden kann.
Hierbei zeigen die letzten drei Punkte \(L‘ \leq_p L\). Mit dem letzten Satz folgt daraus und aus den ersten beiden Punkten dann \(L \in NPC\).
Das Problem ist nun, dass, um im zweiten Schritt des Verfahrens ein \(L‘ \in NPC\) auswählen zu können, man erstmal welche haben muss! Je mehr man hier kennt, desto besser ist es später, aber ein erstes brauchen wir und dort werden wir tatsächlich alle Probleme aus \(NP\) auf dieses reduzieren müssen! (Denn für das erste Problem können wir obiges Verfahren noch nicht anwenden, da der zweite Schritt nicht möglich ist.)
Als erstes \(NP\)-vollständige Problem nehmen wir das auch historisch erste \(NP\)-vollständige Problem nämlich das Erfüllbarkeitsproblem der Aussagenlogik \(\texttt{SAT}\) (für Satisfiability).
Definiton 5.3.7 (SAT)
Das Erfüllbarkeitsproblem der Aussagenlogik ist definiert als das Entscheidungsproblem \(\texttt{SAT}\) mit$$ \texttt{SAT} = \{\langle \phi \rangle \mid \phi \text{ ist eine erfüllbare aussagenlogische Formel}\} $$
Satz 5.3.7
\(\texttt{SAT}\) ist \(NP\)-vollständig.Beweis
Um \(\texttt{SAT} \in NP\) zu zeigen, raten wir gegeben eine Formel \(\phi\) eine Belegung (es gibt \(2^n\) viele bei \(n\) verschiedenen Variablen in \(\phi\)) und verifizieren in Polynomialzeit, ob sie die Formel erfüllt.Um zu zeigen, dass \(\texttt{SAT}\) vollständig ist für \(NP\) müssen wir alle Probleme aus \(NP\) auf \(\texttt{SAT}\) reduzieren. Die Beweisidee ist zu einer Sprache \(L \in NP\) die Turingmaschine \(M\) mit \(L(M) = L\) zu betrachten und alle Kopfbewegungen und damit mögliche Konfigurationsübergänge in einer Formel zu kodieren. Ist diese Formel erfüllbar, gibt es eine akzeptierende Rechnung, sonst nicht. Die genaue Konstruktion ist interessant, führt hier aber zu weit. Man findet den Beweis z.B. im Buch von Hopcroft, Ullman und Motwani.
Hat man nun erstmal ein \(NP\)-vollständiges Problem, so kann man (dem Plan oben entsprechend) nun dieses benutzen, um weitere Probleme als \(NP\)-vollständig nachzuweisen. Der umständliche Weg \emph{alle} \(NP\)-Probleme auf ein neues zu reduzieren entfällt so (bzw. man kriegt dies insb. wegen der Transitivität von \(\leq_p\) geschenkt). Je größer dann der Vorrat an \(NP\)-vollständigen Problemen ist, desto größer ist die Auswahl an Problemen, von denen man eine Reduktion auf ein neues Problem, dessen Komplexität noch unbekannt ist, versuchen kann. (Es gibt natürlich immer die Möglichkeit alle Probleme aus \(NP\) auf ein neues zu reduzieren, aber i.A. wird dies nicht gemacht, sondern wie im Verfahren oben beschrieben vorgegangen.)
Wir wollen neben \(\texttt{SAT}\) noch zwei weitere Probleme als \(NP\)-vollständig voraussetzen. Die Beweise finden sich wieder im Buch von Hopcroft, Ullman und Motwani.
Satz 5.3.9
Die Probleme$$ \texttt{CNF} = \{\langle \phi \rangle \mid \phi \text{ ist eine erfüllbare aussagenlogische Formel in KNF}\} $$
und
$$ \texttt{3CNF} = \{\langle \phi \rangle \mid \phi \in CNF, \text{jede Klausel hat genau drei verschiedene Literale}\} $$
sind \(NP\)-vollständig.
Beweis
\(\texttt{CNF}, \texttt{3CNF} \in NP\) ist klar. Man kann dann \(\texttt{SAT} \leq_p \texttt{CNF}\) und \(\texttt{CNF} \leq_p \texttt{3CNF}\) zeigen (siehe wieder das Buch von Hopcroft, Ullman und Motwani).Neben den eben betrachten \(\texttt{Clique}-\) und \(\texttt{Big-Clique}\)-Problem sind auch die anderen im letzten Abschnitt eingeführten \(NP\)-Probleme, das Mengenpartitonsproblem, das Teilsummenproblem und das Färbungsproblem alle \(NP\)-vollständig. Daneben gibt es noch tausende weitere und für keines dieser Probleme ist ein effizienter Algorithmus (d.h. ein Algorithmus, der in Polynomialzeit läuft) bekannt. Dies bestärkt uns in dem Glauben, dass ein Nachweis von \(L \in NPC\) bedeutet, dass \(L\) nicht in \(P\) liegt. Denn wäre es in \(P\), würden all die tausenden von Probleme, für die kein effizienter Algorithmus gefunden werden konnte, plötzlich in \(P\) sein.
Daher kann man nun, gegeben ein Problem für das man einen Algorithmus entwickeln will, dies zunächst versuchen. Fallen einem aber nach einiger Zeit und etlichem Nachdenken stets nur Algorithmen ein, die \emph{im Prinzip den ganzen Suchraum durchgehen}, so ist das Problem vermutlich \(NP\)-vollständig (oder schlimmer). Dies kann man dann versuchen nachzuweisen. Gelingt dies, kann man die Suche nach einem effizienten Algorithmus zugunsten von anderen Ansätzen verwerfen. Möglichkeiten diese Probleme dennoch zu attackieren sind z.B. Einschränkungen der Eingabe zu betrachten (vielleicht braucht man ja nur mit Bäumen zu arbeiten statt mit allgemeinen Graphen), Approximationsalgorithmen zu entwickeln (mit denen man i.A. nicht das Optimum ermittelt, aber vielleicht einen Wert, der gut genug ist), randomisierte Algorithmen zu entwickeln (die manchmal kein Ergebnis liefern) oder Heuristiken zu entwickeln (bei denen sowohl die Laufzeit als auch die Güte des Ergebnisses meist unklar sind). Diese Möglichkeiten sind Inhalt von weiterführenden Veranstaltungen zur Algorithmik.
