DFAs konstruieren

Download PDF

Üblicherweise ist eine Sprache $M$ gegeben oder wir interessieren uns für eine Menge von Worten $M$, die wir selbst spezifizieren. Dies könnte z.B. die Menge aller Worte sein, die auf $0$ enden oder ähnliches. Die Frage ist dann, wie wir zu dieser Sprache $M$ einen DFA konstruieren können, der $M$ akzeptiert (und später auch ob überhaupt).

Der andere Fall...

Der andere Fall, dass wir einen Automaten $A$ haben und uns für seine akzeptierte Sprache interessieren, tritt viel seltener und überwiegend nur zu didaktischen Zwecken auf. Dieser Fall ist vergleichbar damit, dass man unkommentierten Programmcode erhält und dessen Bedeutung herausfinden muss.

Wie gehen wir nun vor, wenn wir eine Sprache $M$ haben und einen Automaten $A$ mit $L(A) = M$ konstruieren wollen? Dieser Entwurf eines Automaten erfordert von uns Kreativität und lässt sich nicht automatisieren, d.h. es gibt kein Rezept dafür, dem wir folgen können, um am Ende den Automaten $A$ zu haben. Es gibt allerdings Techniken, die man erlernen kann und je nach $M$ vielleicht anwenden kann. Wir wollen nachfolgend zwei solcher Techniken erläutern und jeweils anhand eines Beispiels illustrieren.

Technik 1: Mit dem Speicher arbeiten

Bei der ersten Technik fragen wir uns, was für Informationen wir speichern wollen und wie wir dies mit den Zuständen machen können. Der endliche Automat hat ja eine endliche Menge von Zuständen und diese endliche Menge kann genutzt werden, um endliche viele Informationen zu speichern. Z.B. könnte man sich für das zuletzt gelesene Symbol der Menge $\Sigma = \{0,1\}$ interessieren und dafür zwei Zustände $z_0$ und $z_1$ anlegen. In $z_0$ wechselt man dann, wenn man eine $0$ liest, in $z_1$, wenn man eine $1$ liest. Im Index des Zustands merkt man sich also das zu letzt gelesene Symbol. Wichtig hierbei ist, dass man sich nur endlich viele Informationen merken kann. Man muss also aus der gegebenen Sprache $M$ wichtige Eigenschaften herleiten, die man in den Zuständen speichert und die einem dann tatsächlich bei der Akzeptierung der Worte aus $M$ nützen. Ferner muss es auch möglich sein, die Informationen zu aktualisieren. Oben geschah dies ganz einfach stets beim Lesen des nächsten Symbols.

Wir wollen diese Technik an einem Beispiel verdeutlichen. Sei
$$ M := \{ w \in \{0,1\}^* \mid \text{ $|w|_0$ ist gerade und $|w|_1$ ist ungerade} \} $$ In $M$ sind also jene Worte aus $0$en und $1$en, die eine gerade Anzahl an $0$en und eine ungerade Anzahl an $1$ en enthalten. Zum Beispiel ist also $01110 \in M$ (zwei $0$en und drei $1$en), nicht aber $0101$ (die Anzahl der $0$en ist zwar gerade, die der $1$en aber auch).

Wie konstruieren wir hierzu nun einen DFA? Dazu muss man sich überlegen, welche speziellen Eigenschaften ein Wort aus $M$ hat und ob man sich diese Eigenschaften mit endliche vielen Informationen merken kann. Bevor unten ein Lösungsvorschlag kommt, kann man an dieser Stelle einmal selbst ausprobieren, ob man auf eine Lösung kommt.

Eine Beispiellösung

Ein Wort $w \in M$ hat die Eigenschaft gerade viele $0$en und ungerade viele $1$en zu enthalten. Wenn wir nun die Anzahl der $0$en und der $1$en zählen und diese Information im Zustand speichern wollen, dann brauchen wir unendlich viele Zustände, da wir ja Hundert oder auch Tausend oder auch Zehntausend $0$en lesen können. Dieser Ansatz geht also nicht. Wir brauchen aber auch gar nicht die genaue Anzahl der $0$en und $1$en. Es genügt ja zu wissen, ob wir bis zu einem bestimmten Zeitpunkt gerade oder ungerade viele $0$en gesehen haben. Dies sind zwei Informationen (gerade oder ungerade) für zwei Symbole ([/latex]0[/latex] und $1$), also brauchen wir insgesamt nur vier Zustände für die vier Fälle gerade viele $0$en und gerade viele $1$en, gerade viele $0$en und ungerade viele $1$en usw. Zudem können wir die gespeicherten Informationen leicht aktualisieren, wenn der Automat eine $0$ oder eine $1$ liest.

Um dies im Detail auszuführen nehmen wir als Zustände $z_{gg}, z_{ug}, z_{gu}$ und $z_{uu}$. Ein $u$ im Index steht dabei für ungerade, ein $g$ für gerade. Das erste Symbol steht für die $0$en, das zweite für die $1$en. Der Zustand $z_{ug}$ soll also erreicht werden, wenn wir ungerade viele $0$en und gerade viele $1$en gelesen haben. Als Startzustand macht dann $z_{gg}$ Sinn, da wir null gelesene $0$en und null gelesene $1$en als gerade viele $0$en und $1$en ansehen wollen. Der Endzustand ist mit Blick auf die Menge $M$ dann $z_{gu}$. Damit haben wir als Zustandsübergangsdiagramm des Automaten $A$ bisher den gezeigten Automaten.

Wenn wir nun in $z_{gg}$ sind und eine $0$ lesen, dann ändert sich die gespeicherte Information, dass wir gerade viele $0$en gelesen haben, denn es kommt ja eine dazu und damit sind es nun ungerade viele. Die gespeicherte Information zu den $1$en hingegen ändert sich nicht. Wir machen also eine $0$-Kante in den Zustand $z_{ug}$, da wir nun ungerade viele $0$en und weiterhin gerade viele $1$en gelesen haben. Ebenso machen wir eine $1$-Kante von $z_{gg}$ nach $z_{gu}$. Dies ergibt als Automat nun folgendes Bild.

Man überlegt sich dann schnell, dass für die eben eingezeichneten Kanten auch Kanten mit der gleichen Beschriftung zurück nötig sind, da gerade wieder die gleiche gespeicherte Information geändert werden muss. Ebenso kann man sich für die verbleibenden Zustände und Symbole die Kanten überlegen. Ist man z.B. in $z_{uu}$, so hat man ungerade viele $0$en und $1$en gelesen und ein Lesen von $0$ führt dann in $z_{gu}$, da man dann gerade viele $0$en und weiterhin ungerade viele $1$en gelesen hat. Insgesamt ergibt sich damit der abgebildete Automat.

Wir sind mit der Konstruktion fertig, da wir einen Startzustand haben, eine Endzustandmenge und für jedes Symbol Kanten aus jedem Zustand heraus (der Automat ist also sogar vollständig). Es ist nun aber wie im vorherigen Abschnitt zunächst nur eine Behauptung, dass $L(A) = M$ tatsächlich gilt. Dies ist nun noch zu beweisen! Dazu kann man sich zuerst überlegen, dass für jeden Zustand und alle Kanten gilt, dass die Informationen richtig neu gesetzt werden. Wenn man also in einem Zustand $z_{xy}$ ist und mit einer $0$-Kante den Zustand $z_{x'y}$ erreicht bzw. mit einer $1$-Kante den Zustand $z_{xy'}$, dann wird $x$ richtig in $x'$ bzw. $y$ richtig in $y'$ geändert. Exemplarisch haben wir das bereits oben für einige argumentiert. Man kann am Zustandsdiagramm sehen, dass dies tatsächlich für alle Zustände und alle Kanten gilt. Dies erlaubt gleich die Formulierung, dass bestimmte Dinge "nach Konstruktion" gelten. Wir zeigen nun $L(A) = M$.

Sei $w \in M$, dann kann $w$ nach Konstruktion (der Automat ist vollständig) zu Ende gelesen werden. Nach Konstruktion der Zustände und der Zustandsübergänge (s.o.) enden wir dann in $z_{gu}$ (da $w$ eine gerade Anzahl von $0$en und eine ungerade Anzahl von $1$en enthält) und akzeptieren. Also ist auch $w \in L(A)$.
Sei $w \in L(A)$. Da $w$ akzeptiert wird, muss $A$ in $z_{gu}$ enden. Dies ist aber nach Konstruktion (s.o.) gleichbedeutend damit, dass $w$ gerade viele $0$en und ungerade viele $1$en enthält. Damit gilt auch $w \in M$.

Die Formulierung "nach Konstruktion" macht hier Sinn, da wir oben die Idee sauber beschrieben haben und für alle Zustände und Kanten erklären können was passiert. Zudem ist der Automat hinreichend klein und übersichtlich, so dass man dies hier so akzeptieren kann. Noch sauberer gelingt der Beweis mit einer vollständigen Induktion über die Wortlänge. Hier wird dann ebenfalls oben ausgeführtes zu den Zuständen und den Zustandsübergängen benutzt. Man kann aber besser argumentieren, warum man z.B. bei der ersten Beweisrichtung tatsächlich in $z_{gu}$ landet. Diese Stelle wäre oben noch angreifbar.

Wir beweisen $L(A) = M$ noch einmal mit Induktion über die Wortlänge. Das schwierige ist dann insb. eine gute Induktionsbehauptung aufzustellen.

Sei $w = w_1 \ldots w_n \in \{0,1\}^*$ (mit $w_1, \ldots, w_n \in \{0,1\}$). Wir zeigen mittels Induktion über die Wortlänge $n$: $w$ kann von $A$ gelesen werden und $A$ endet in $z_{gg}$, wenn $|w|_0$ und $|w|_1$ gerade sind, in $z_{gu}$, wenn $|w|_0$ gerade und $|w|_1$ ungerade ist, in $z_{ug}$, wenn $|w|_0$ ungerade und $|w|_1$ gerade ist und in $z_{uu}$, wenn $|w|_0$ und $|w|_1$ ungerade sind.

Induktionsanfang: Sei $n = 0$, dann ist $w = \lambda$, $|w|_0$ und $|w|_1$ sind gerade und $A$ kann $w$ lesen und endet in $z_{gg}$ wie gewünscht.

Induktionsannahme: Die Induktionsbehauptung gelte für ein $n \geq 0$
.

Induktionsschritt: Sei nun $w = w_1 \ldots w_n w_{n+1}$ ein Wort der Länge $n+1$. Wir wenden auf $w' := w_1 \ldots w_n$ die Induktionsannahme an. $A$ kann $w'$ also lesen und endet in einem seiner vier Zustände, je nachdem, ob $|w'|_0$ und $|w'|_1$ gerade oder ungerade sind. Wir machen eine Fallunterscheidung. Angenommen $w'$ hat eine gerade Anzahl von $0$en und $1$en und angenommen $w_{n+1}$ ist eine $0$, dann ist $|w|_0$ ungerade ([/latex]|w'|_0[/latex] haben wir als gerade angenommen und $w_{n+1}$ als $0$, damit ist $|w|_0$ ungerade) und $|w|_1$ gerade.

Wir müssen nun zeigen, dass $w$ von $A$ gelesen werden kann und dass $A$ nach Lesen von $w$ in $z_{ug}$ ist. Nach der Induktionsannahme und da $|w'|_0$ und $|w'|_1$ gerade sind, kann $A$ das Teilwort $w'$ lesen und ist nach Lesen von $w'$ in $z_{gg}$. Nach Konstruktion überführt $w_{n+1} = 0$ dann $A$ nach $z_{ug}$. Damit haben wir das Gewünschte für diesen Fall bereits gezeigt.

Analog behandelt man den Fall, dass $w_{n+1}$ eine $1$ ist und dann ganz analog die Fälle, dass $A$ nach Lesen von $w'$ in einem der anderen drei Zustände ist. Insgesamt sind hier also acht Fälle zu behandeln (die vier Zustände, in denen $A$ nach Lesen von $w'$ ist sowie dann jeweils $w_{n+1} = 0$ oder $w_{n+1} = 1$).

Damit haben wir die Induktionsbehauptung gezeigt. Sei nun $w \in M \subseteq \{0,1\}^*$. Dann wissen wir, dass $|w|_0$ gerade und $|w|_1$ ungerade ist. Nach dem eben bewiesen überführt uns $w$ also in $z_{gu}$ und da dies ein Endzustand ist, gilt $w \in L(A)$.

Dies sieht alles sehr ähnlich zu obigem aus. Die Konstruktionsidee findet sich im Induktionsschritt wieder. Insgesamt ist der Beweis so aber sauberer als der oben zuerst geführte. In diesem kleinen Beispiel hätte der oben zuerst geführte aber auch genügt. Der Leser muss sich dann aber an der Stelle "Nach Konstruktion der Zustände und der Zustandsübergänge (s.o.) enden wir dann in $z_{gu}$"selbst davon überzeugen können, dass die Aussage stimmt. Das ist bei diesem kleinen Beispiel noch recht eingängig. Mit einer Induktion aber stichhaltiger gezeigt.
Sei $w \in L(A)$. Wir wollen $w \in M$ zeigen. Betrachten wir noch einmal obige Induktionsbehauptung, dann haben wir dort wenn-dann-Formulierungen der Art \emph{wenn $|w|_0$ und $|w|_1$ gerade sind, dann endet $A$ in $z_{gg}$}. Da es bezüglich gerader und ungerader Anzahl der $0$en und $1$en nur die vier Fälle für Worte $w \in \{0,1\}^*$ gibt, sind dies sogar genau-dann-wenn-Beziehungen, d.h. wir können aus obigen sofort auch schlussfolgern, dass z.B. $|w|_0$ und $|w|_1$ gerade sind, wenn $A$ in $z_{gg}$ endet. (Angenommen $|w|_0$ und $|w|_1$ wären nicht beide gerade, dann würde aus der oben bewiesene Induktionsbehauptung folgen, dass $A$ nicht in $z_{gg}$, sondern in einem der anderen Zustände endet. Wir sind ja aber gerade davon ausgegangen, dass wir in $z_{gg}$ enden und hätten hier einen Widerspruch.) Mit dieser Überlegung folgt der Beweis nun ganz schnell. Sei $w \in L(A)$, dann enden wir in $z_{gu}$, da dies der einzige Endzustand ist. Dann aber folgt aus dem eben beschriebenen sofort, dass $|w|_0$ gerade und $|w|_1$ ungerade ist und damit $w \in M$ gilt. (Diese Richtung erscheint deswegen so kurz, weil wir im Grunde genommen oben bei der Induktionsbehauptung auch "genau dann, wenn"-Beziehungen gezeigt haben und daher die dortige Aussage hier benutzen können.)

Damit sind wir mit diesem Beispiel fertig.

Wir wollen noch anmerken, dass bei dieser Technik bisweilen ein Teil konstruiert wird, der dann gar nicht benötigt wird. Dies kann passieren, wenn man zunächst Speicherinhalte berücksichtig, von denen man später bemerkt, dass man sie gar nicht braucht, weil sie (doch) nicht entstehen können. Dies ist aber nicht weiter tragisch, man würde sich dann einfach im Nachhinein auf die initiale Zusammenhangskomponente (also jenen Teil des Automaten, der vom Startzustand aus erreichbar ist) einschränken.

Technik 2: On-the-fly-Entwurf

Die zweite Technik, die wir kennenlernen wollen ist eine „on-the-fly“-Technik. Man fängt hier mit dem Startzustand an und überlegt sich dann für jedes Eingabesymbol $x \in \Sigma$, ob einem dieses weitere Informationen bringt, die man speichern will oder nicht. Der so entstehende Automat ist stets initial zusammenhängend und vollständig. Man muss bei der Konstruktion aber darauf achten, dass man irgendwann zu Zuständen zurück kommt, die man bereits generiert hatte, sonst generiert man unendlich viele Zustände.

Wir wollen diese Technik wieder an einem kleinen Beispiel demonstrieren. Sei $$M := \{0,1\}^* \{1\} = \{w \in \Sigma^* \mid \exists v \in \Sigma^*: w = v1\}$$ In $M$ sind also jene Worte aus $0$en und $1$en, die auf $1$ enden. Beispielsweise ist $0101$ (letztes Symbol ist $1$) enthalten, nicht aber $1010$ (letztes Symbol ist $0$, nicht $1$).

Wir könnten mit der ersten Konstruktionsmethode hierzu einen Automaten bauen, indem wir uns im Speicher merken, was das zuletzt gelesene Symbol ist. Dazu brauchen wir nur zwei Zustände, den das zuletzt gelesene Symbol ist entweder $0$ oder $1$. Wir wollen aber nachfolgend die On-the-fly-Technik illustrieren. Man kann trotzdem einmal probieren zunächst selbst einen Automaten zu bauen und seine Richtigkeit zu beweisen, bevor man weiter liest.

Eine Beispiellösung

Wir starten mit einem Startzustand (denn jeder DFA hat einen Startzustand) und fragen uns nun für jedes Symbol aus $\Sigma$, was wir mit diesem Symbol anstellen können.

Bei einer $0$ wissen wir nicht, ob das letzte Symbol eine $1$ ist (vielleicht haben wir sogar gerade das letzte Symbol gelesen). Auf jeden Fall wollen wir also nicht akzeptieren. Wir könnten nun einen neuen Zustand erstellen und eine $0$-Kante dorthin machen. Bei genauerer Betrachtung merkt man aber, dass dieser Zustand im Vergleich zu $z_0$ keinen Mehrwert hat. Wir wissen im Grunde genauso viel wie vorher. Daher machen wir besser eine $0$-Schleife an $z_0$.

Bei einer $1$ hingegen müssen wir den Zustand wechseln. Dies könnte ja das letzte Symbol des Wortes sein und dann wollen wir akzeptieren. Wir machen uns also einen neuen Zustand und lassen dort eine $1$-Kante von $z_0$ hinführen. Dies muss zudem ein Endzustand sein, denn diese $1$ könnte ja das letzte Symbol des Wortes sein und dann wollen wir akzeptieren.

Mit dem Zustand $z_0$ sind wir nun fertig, denn wir haben für jedes Symbol eine Kante. Wir haben allerdings einen neuen Zustand $z_1$ erzeugt und müssen uns nun fragen, was hier für die einzelnen Symbole von $\Sigma$ passiert.

Wenn wir in $z_1$ sind und eine $1$ lesen, dann ist weiterhin das letzte gelesene Symbol eine $1$ und wenn dies sogar das letzte Symbol des Wortes ist, wollen wir akzeptieren. Wir verbleiben also in $z_1$. Wichtig hier ist wieder zu erkennen, dass es nicht nötig ist, einen neuen Zustand einzuführen, sondern dass wir auch nach Lesen weiterer $1$en in $z_1$ verbleiben können, da wir hier genau die Informationen haben, die wir brauchen.

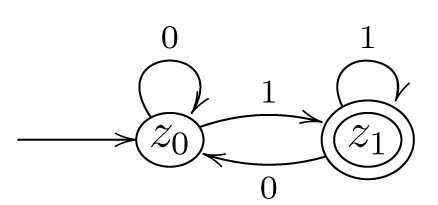
Lesen wir aber hingegen eine $0$, so müssen wir $z_1$ verlassen, denn nun ist das letzte gelesene Symbol keine $1$ mehr und wenn das Wort mit dieser $0$ endet, dann wollen wir ganz bestimmt nicht akzeptieren. Wir könnten nun einen neuen Zustand $z_2$ machen und dort die $0$-Kante von $z_1$ hinführen. Dann hätten wir einen weiteren Zustand und müssten uns wieder fragen, was hier bei einer $0$ oder bei einer $1$ passiert. Bemerkt man aber an dieser Stelle, dass man wieder die gleichen Informationen hat wie in $z_0$, so kann man dorthin wechseln und spart sich dies. Der Automat ist dann fertig, da man für alle Zustände Kanten für alle Symbole hat. Der Automat ist also vollständig.

Wie immer muss nun aber noch $L(A) = M$ bewiesen werden. Dies geht allerdings hier deutlich einfacher als in dem vorherigen Beispiel. Man beachte, dass der Automat vollständig ist (also jedes Wort $w \in \{0,1\}^*$ lesen kann) und dass jede $1$-Kante nach $z_1$ führt.

Sei $w = v1 \in M$ mit $v \in \{0,1\}^*$. Da der Automat vollständig ist, können $v$ und $w$ auf jeden Fall ganz gelesen werden. Da $w$ auf $1$ endet, muss der Automat mit dieser letzten $1$ nach Konstruktion (jeder Zustand hat eine $1$-Kante nach $z_1$) in den Zustand $z_1$ wechseln – oder anders: egal wo wir nach Lesen von $v$ sind, die folgende $1$ führt uns nach $z_1$. Mit $z_1 \in Z_{end}$ folgt $w \in L(A)$.
Sei $w \in L(A)$. Dann muss nach Konstruktion das Wort auf $1$ enden, da $z_1$ der einzige Endzustand ist und alle Kanten nach $z_1$ mit $1$ beschriftet sind. Dann ist aber sofort auch $w \in M$.

Damit sind wir auch mit diesem Beispiel fertig.

Wir betonen noch einmal, dass es bei dieser Konstruktionsmethode kritisch ist irgendwann zu merken, wann bereits vorhandene Zustände benutzt werden können – und im besten Fall auch, wofür sie stehen; bspw. kann man oben $z_x$ mit „letztes gelesenes Symbol ist $x$“ identifizieren ($x \in \{0,1\}$). Ansonsten konstruiert man immer weiter Zustände und der Automat wird nicht endlich.

Ein kompliziertes Beispiel

Wir wollen zum Abschluss dieses Abschnittes noch ein komplizierteres Beispiel betrachten. Bei einigen der oben bisher betrachteten Mengen und Automaten mag der ein oder andere denken, dass man die Lösung doch gleich sehe und warum man dann so umständlich argumentieren müsse? Die bisherigen Beispiele sollten das Vorgehen einüben und waren deswegen nicht zu kompliziert gewählt, damit man nicht sofort von umständlichen Argumentationen überwältigt wird. So konnte man sich auf das Vorgehen an sich konzentrieren und die Argumentationen blieben vergleichsweise übersichtlich. Damit wir aber noch einmal sehen können, dass die Argumente durchaus komplexer werden können, betrachten wir nun noch ein komplizierteres Beispiel.

Sei zunächst $$ \Sigma = \{ \begin{bmatrix} x \\ y \\ z \end{bmatrix} \mid x,y,z \in \{0,1\} \}. $$ Ein Symbol aus $\Sigma$ ist also eine Art Vektor mit drei Elementen oder für uns nachfolgend besser mit drei Zeilen. Ein Wort aus $\Sigma^*$ kann dann nämlich als drei Zeilen mit $0$en und $1$en gesehen werden. Im Wort
$$ \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}
\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}
\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} $$
ist bspw. die erste Zeile $0 1 1 0$, die zweite Zeile $0 1 1 1$ und die dritte Zeile $1 1 0 1$. Wir interpretieren nun jede Zeile als Binärzahl und betrachten die Sprache $$ Sum = \{ w \in \Sigma^* \mid \text{ die unterste Zeile ist Summe der oberen Zeilen} \} $$ In dem oben notierten Wort aus vier Symbolen ist dies der Fall, es wäre also in $Sum$. Wir fragen nun: Ist $Sum$ regulär?

Ein erster Hinweis

Um ein Gefühl für die Sprache zu bekommen, kann man mit einigen kurzen Worten z.B. der Länge drei oder vier arbeiten und sich überlegen, was ein Automat tun müsste, wenn er diese Worte akzeptieren oder ablehnen sollte. An dieser Stelle kann man bemerken, dass die Behandlung des Übertrags problematisch ist. Der Automat liest das Wort ja von links nach rechts, kann hier aber scheinbar nicht bemerken, dass an einer Stelle eine richtige Rechnung stattfindet, da diese ggf. nur richtig ist, wenn man einen Übertrag hat, der ja aber erst später in dem Wort kommt. Würden wir das Wort von hinten lesen, wäre es einfacher. Wir könnten dann an jeder Stelle des Wortes, ganz so wie wir es beim schriftlichen Addieren machen, überprüfen, ob die Rechnung an dieser Stelle richtig ist und ob es einen Übertrag gibt. Wir ändern daher zunächst die Aufgabenstellung. Statt $Sum$ zu betrachten, betachten wir nun die Menge aller Wörter $w$, die umgedreht (also von rechts nach links gelesen) gerade in $Sum$ sind. Diese Menge nennen wir $Sum^R$ ($R$ für Rückwärts). Hat man z.B. ein Wort $w = abb$, dann ist $w^R = bba$ und hat man eine Menge von Worten $M$, dann ist $M^R = \{w^R \mid w \in M\}$.

Statt nun zu versuchen $Sum$ als regulär nachzuweisen, wollen wir nun also zeigen, dass $Sum^R$ regulär ist. (Später werden wir sehen, dass für jede reguläre Sprache $M$, $M^R$ regulär ist (und umgekehrt). Daraus folgt dann, dass $Sum$ regulär ist. Hier wollen wir es jetzt aber dabei belassen, darüber nachzudenken, ob $Sum^R$ regulär ist.)

Die Idee und der Automat

Mit der Idee von eben, $Sum^R$ zu betrachten gelangen wir weiter. Wir lesen nun quasi eine binäre Addition von rechts nach links und können an jeder Stelle prüfen, ob richtig gerechnet wird. Falls dabei ein Übertrag auftritt, dann merken wir uns diesen im Zustand. Da es nur die Möglichkeit für einen Übertrag von $0$ oder von $1$ gibt, sind dies nur zwei Informationen und wir kommen mit endlich vielen Zuständen aus! Wir beginnen in einem Startzustand $z_0$, mit dem wir gleichzeitig Übertrag $0$ symbolisieren wollen. Kommt nun als erster Buchstabe ein Vektor wie $(0,0,0)$ oder $(1,0,1)$ (für die bessere Lesbarkeit schreiben wir die Vektoren hier als Zeilen; das erste Element im Vektor entspricht der ersten Zeile, das zweite Element der zweiten Zeile und das dritte Element der dritten Zeile), so können wir in $z_0$ bleiben, denn in beiden Fällen ist die dritte Zeile (bzw. das dritte Element, in der Schreibweise als Tupel von eben) Summe der ersten beiden Zeilen (der ersten beiden Elemente) und es gibt keinen Übertrag. Entsprechendes gilt für $(0,1,1)$.

Bei $(1,1,0)$ hingegen stimmt zwar die Addition, wir haben aber einen Übertrag, d.h. wir müssen den Zustand wechseln. Hierfür erstellen wir einen neuen Zustand $z_1$, in dem wir uns merken, dass wir Übertrag $1$ haben. Alle anderen Symbole wie z.B. $(0,0,1)$ oder $(1,1,1)$ entsprechen Fehlern in der Rechnung, denn wenn wir keinen Übertrag haben (wir sind ja noch in $z_0$), dann ist $0 + 0$ nicht $1$ und $1+1$ auch nicht. Analog für die anderen beiden fehlenden Symbole. Diese vier Symbole führen also in einen neuen (Fehler-)Zustand. Der Fehlerzustand hat zudem für jedes $x \in \Sigma$ eine Kante zu sich selbst. Hier kann das Wort also zu Ende gelesen werden, wird aber nicht akzeptiert.

In $z_1$ haben wir nun Übertrag $1$ und wir gehen wieder alle Symbole durch und prüfen, ob die Rechnung an dieser Stelle stimmt. Dabei beachten wir aber den Übertrag von $1$. So bleiben wir z.B. mit $(1,0,0)$ in $z_1$, denn $1 + 0$ ist zwar $1$, aber wenn nun noch der Übertrag $1$ hinzukommt, so haben wir richtigerweise in der dritten Zeile eine $0$ und merken uns wieder den Übertrag von $1$ (in $z_1$). Analog für $(0,1,0)$ und $(1,1,1)$. Das Symbol $(0,0,1)$ führt nun zurück zu $z_0$, denn $0+0$ plus den Übertrag ergibt $1$, aber wir haben nun keinen Übertrag mehr, den wir uns merken müssten und gehen zurück nach $z_0$. Die anderen vier Symbole führen wieder in den Fehlerzustand, da hier ein Fehler in der Rechnung aufgetreten ist. Zuletzt wählen wir noch $z_0$ als Endzustand, da wir nur Worte akzeptieren wollen, die korrekte Rechnungen sind, bei denen also auch kein Übertrag mehr besteht. Dies ergibt den abgebildeten Automaten. Dieser ist schon recht kompliziert und seine Korrektheit ist nicht sofort ersichtlich. Daher ist hier ein nachvollziehbarer Beweis von $L(A) = Sum^R$ dringend nötig.

Der Beweis

Wir teilen den Beweis wieder in zwei Richtungen auf. In beiden Richtungen führen wir einen induktiven Beweis über die Wortlänge.

Wir zeigen per Induktion über die Wortlänge $n$: Für $w = w_1 \ldots w_n$ gilt:
- Wenn $w$ eine korrekte Rechnung mit Übertrag 0 ist, dann liest $A$ das Wort $w$ und endet in $z_0$.
- Wenn $w$ eine korrekte Rechnung mit Übertrag 1 ist, dann liest $A$ das Wort $w$ und endet in $z_1$.
Wobei wir hier mit korrekte Rechnung meinen, dass in $w^R$ die erste und zweite Zeile zusammenaddiert gerade die dritte Zeile ergibt, wobei am Ende noch ein Übertrag von $0$ oder $1$ bestehen kann. Man beachte insb. dass wir von einer korrekten Rechnung sprechen, auch wenn das Wort noch umgedreht werden muss.

Induktionsanfang: $w = w_1$. Nur in den Fällen $(0,0,0), (1,0,1)$ und $(0,1,1)$ ist $w$ eine korrekte Rechnung mit Übertrag $0$. $A$ liest hier $w$ und endet in $z_0$. In dem Fall $(1,1,0)$ ist $w$ eine korrekte Rechnung mit Übertrag $1$. $A$ liest in diesem Fall $w$ und endet in $z_1$. In den übrigen Fällen $(1,0,0), (0,1,0), (0,0,1)$ und $(1,1,1)$ ist $w$ keine korrekte Rechnung und es ist nichts zu zeigen. (Wir sind hier also einfach alle Möglichkeiten für $w_1 \in \Sigma$ durchgegangen und haben gezeigt, dass die geforderten "wenn ... dann"-Beziehungen gelten.)

Induktionsannahme: Gelte die Behauptung für ein $n \geq 1$.

Induktionsschritte: Sei nun $w = w_1 \ldots w_{n+1}$ ein Wort der Länge $n+1$. Wir unterscheiden die zwei Fälle.
1. $w = w_1 \ldots w_{n+1}$ ist eine korrekte Rechnung mit Übertrag $0$. Wir müssen zeigen, dass $A$ das Wort $w$ lesen kann und dann in $z_0$ ist. Wir betrachten $w' := w_1 \ldots w_n$. Diese Rechnung muss auch korrekt sein, da $w_1 \ldots w_{n+1}$ korrekt ist. D.h. $w'$ ist eine korrekte Rechnung und hat Übertrag $0$ oder $1$. Wir wenden auf $w'$ die Induktionsannahme an. Hat $w'$ Übertrag $0$ so enden wir (nach Induktionsannahme) in $z_0$. Da $w = w_1 \ldots w_{n+1}$ eine korrekte Rechnung mit Übertrag $0$ ist, kann, da auch $w'$ eine korrekte Rechnung mit Übertrag $0$ ist, $w_{n+1}$ nur eines der Symbole $(0,0,0), (1,0,1)$ oder $(0,1,1)$ sein, also gerade jene Symbole, die im Automaten Schleifen an $z_0$ sind. $A$ bleibt also in $z_0$, was wir ja gerade zeigen wollten.
  
  Hat $w' = w_1 \ldots w_n$ Übertrag $1$, so enden wir nach Induktionsannahme in $z_1$. Damit $w$ nun Übertrag $0$ hat, gibt es für $w_{n+1}$ nur den Fall $(0,0,1)$. Diese Kante führt uns im Automaten aber wieder nach $z_0$, womit wir insgesamt gezeigt haben, dass $A$ das Wort $w$ lesen kann und in $z_0$ endet (ausgehend von einer Korrekten Rechnung $w$ mit Übertrag $0$).
2. Im zweiten Fall ist $w = w_1 ... w_{n+1}$ eine korrekte Rechnung mit Übertrag $1$. Wir müssen nun zeigen, dass $A$ das Wort $w$ lesen kann und dann in $z_1$ ist. Wie eben betrachten wir $w' := w_1 \ldots w_n$. $w'$ muss nun ebenfalls wieder korrekt sein und hat Übertrag $0$ oder $1$. Hat $w'$ Übertrag $0$, so liest $A$ nach Induktionsannahme das Wort $w'$ und endet in $z_0$. Nur $w_{n+1} = (1,1,0)$ führt nun dazu, dass $w$ eine korrekte Rechnung mit Übertrag $1$ ist. Dieses Symbol kann $A$ lesen und ist dann in $z_1$, was wir in diesem Fall ja gerade wieder zeigen wollten. Hat $w'$ hingegen Übertrag $1$, so liest $A$ das Wort $w'$ nach Induktionsannahme und ist dann in $z_1$. Nun muss $w_{n+1}$ eines der Symbole $(1,0,0), (0,1,0)$ oder $(1,1,1)$ sein, damit $w$ eine korrekte Rechnung mit Übertrag $1$ ist. Diese Symbole überführen den Automaten $A$ aber gerade von $z_1$ nach $z_1$ und damit haben wir auch hier gezeigt, dass $A$ das Wort $w$ lesen kann und dann in $z_1$ ist.
Damit ist die Induktionsbehauptung bewiesen.

Sei nun $w \in Sum^R$, dann wissen wir dass $w$ in der Formulierung der Induktionsbehauptung eine korrekte Rechnung mit Übertrag $0$ ist. Aus dem eben bewiesenen folgt dann, dass $A$ das Wort $w$ lesen kann und dann in $z_0$ ist. Da $z_0$ ein Endzustand ist, akzeptieren wir und wir haben $w \in L(A)$. Damit ist $Sum^R \subseteq L(A)$ gezeigt.
Für die Rückrichtung, könnten wir eine weitere Induktionsbehauptung aufstellen, die diesmal von der Rechnung des Automaten ausgeht. Diese könnte wie folgt lauten: Liest $A$ das Wort $w = w_1 ... w_n$, so gilt: Wenn $A$ in $z_0$ endet, so ist $w$ eine korrekte Rechnung mit Übertrag $0$, wenn $A$ in $z_1$ endet, so ist $w$ eine korrekte Rechnung mit Übertrag $1$ und wenn $A$ in $z_e$ endet, so ist $w$ eine inkorrekte Rechnung. Dies könnte man ähnlich wie eben beweisen. Man kann aber erkennen, dass dies im Kern gerade die Umkehrungen der "wenn ... dann"-Beziehungen in der ersten Induktionsbehauptung sind. Daher werfen wir noch einmal einen Blick auf diese. Wenn wir dort als dritten Fall noch hinzunehmen
- Wenn $w$ eine inkorrekte Rechnung ist, dann liest $A$ das Wort $w$ und endet in $z_e$.
so müssen wir lediglich im Induktionsanfang noch ausführen, dass die verbleibenden Symbole inkorrekte Rechnungen sind und den Automaten nach $z_e$ führen und im Induktionsschritt kommt der dritte Fall hinzu, dass $w$ eine inkorrekte Rechnung ist. Hier zeigt man aber auch schnell, dass wir in $z_e$ enden. Entweder ist schon die kürzere Rechnung $w'$ eine inkorrekte Rechnung und wir verbleiben in $z_e$ oder wir gelangen von $z_0$ oder $z_1$ nach $z_e$, wenn $w_{n+1}$ für die inkorrekte Rechnung sorgt.

Haben wir dies nun bewiesen, so decken die drei Fälle, dass $w$ eine korrekte Rechnung mit Übertrag $0$ oder $1$ ist und dass $w$ eine inkorrekte Rechnung ist, alle Möglichkeiten für $w$ ab, d.h. aus den "wenn ... dann"-Beziehungen folgen sofort "genau dann, wenn"-Beziehungen es gilt also sogar
- $w$ ist eine korrekte Rechnung mit Übertrag 0 genau dann, wenn $A$ das Wort $w$ liest und in $z_0$ endet.
- $w$ ist eine korrekte Rechnung mit Übertrag 1 genau dann, wenn $A$ das Wort $w$ liest und in $z_1$ endet.
- $w$ ist eine inkorrekte Rechnung genau dann, wenn $A$ das Wort $w$ liest und in $z_e$ endet.
Damit folgt nun ganz schnell auch die Teilmengenbeziehung $L(A) \subseteq Sum^R$. Sei dazu $w \in L(A)$, dann liest $A$ also $w$ und endet in $z_0$. Nach obigem ist dann $w$ eine korrekte Rechnung mit Übertrag $0$, also $w \in Sum^R$.

Dadurch, dass wir uns soviel Arbeit bei der Induktion(sbehauptung) gemacht haben, gingen die beiden Teilmengenbeziehungen dann ganz schnell.

Damit haben wir $L(A) = Sum^R$ bewiesen. Wir wissen nun zwar noch nicht, ob auch $Sum$ regulär ist. Dies wird aber ganz schnell aus der später folgenden Behandlung von Abschlusseigenschaften folgen.

Dieses kompliziertere Beispiel schließt diesen Abschnitt ab. Man beachte, wie hier wieder
eine Induktion über die Wortlänge als Beweistechnik eingesetzt wurde.

Wiederholung

Zusammengefasst haben wir in diesem Abschnitt zwei Techniken zur Konstruktion von DFAs kennengelernt und an Beispielen betrachtet.

Die erste Technik beruht darauf, sich zu einer gegebenen Sprache $M$ zu überlegen, mit welchen Informationen man arbeiten kann, um Worte aus $M$ identifizieren zu können, und wie man diese Informationen aktualisieren kann. Wichtig ist hierbei, dass man nur endliche viele Informationen hat, damit endlich viele Zustände ausreichen, um diese zu speichern, und dass diese durch die Kantenübergänge gut aktualisiert werden können. Manchmal wird bei dieser Technik ein Teil konstruiert, der gar nicht vom Startzustand aus erreichbar ist. Dieser Teil kann dann später entfernt werden.

Die zweite Technik beruht darauf, sich schrittweise zu überlegen, was in jedem Zustand bei jedem Eingabesymbol passiert. Man beginnt hier im Startzustand und erzeugt dann sukzessive weitere Zustände, sofern nötig. Kritisch hier ist zu bemerken, wann man von einem Zustand zu einem bereits generierten Zustand zurück kann. Nur dann bricht das Verfahren ab. Sonst generiert man immer weiter neue Zustände. Die mit der zweiten Technik erstellten endlichen Automaten sind im Allgemeinen initial zusammenhängend und vollständig.

Egal wie man nun zu einem Automaten $A$ kommt. Immer gilt: $L(A) = M$ ist bisher nur eine Behauptung, die dann noch zu zeigen ist. In den Beispielen haben wir die Argumentation "nach Konstruktion" gesehen und einen Induktionsbeweis über die Wortlänge. Die Formulierung "nach Konstruktion" ist oft nützlich, sollte aber nur gewählt werden, wenn man Dinge tatsächlich schnell am Diagramm sehen kann oder wenn man vorher die Idee der Konstruktion gut erläutert hat und hieraus tatsächlich etwas abgeleitet werden kann. Wenn man z.B. einen Automaten mit zwei Endzuständen $z_5$ und $z_9$ hat, dann kann man gut sagen, dass man nach Konstruktion bei einem akzeptierten Wort in $z_5$ oder $z_9$ endet. Dies kann man gut ablesen. Wenn man aber einfach sagt, dass man jedes Wort einer Sprache $M$ nach Konstruktion akzeptiert, dann ist dies in den meisten Fällen zu wenig.

Wenn die Automaten komplizierter werden, dann hilft einem oft ein Induktionsbeweis über die Wortlänge. Man kann dann im Induktionsschritt meist ausnutzen, dass man nach Lesen der ersten $n$ Buchstaben in einem der Zustände ist und die Eigenschaft dieses Zustands nutzen (z.B. dass man in diesem Zustand nur endet, wenn das bisherige Wort gerade viele $0$en hat oder ähnliches; was man hier nutzen kann, hängt von der Induktionsbehauptung ab, die man zeigen will). Danach ist es dann oft möglich mit der Konstruktionsidee zu arbeiten und hier kann dann ggf. auch wieder auf die Konstruktion verwiesen werden.

Hier ein paar Fragen zur Konstruktion von DFAs.

Der andere Fall...

Technik 1: Mit dem Speicher arbeiten

Eine Beispiellösung

Technik 2: On-the-fly-Entwurf

Eine Beispiellösung

Ein kompliziertes Beispiel

Ein erster Hinweis

Die Idee und der Automat

Der Beweis

Wiederholung

Quiz-Zusammenfassung

Informationen

Ergebnis

Kategorien

1. Frage

2. Frage