In diesem Kapitel wollen wir den endlichen Automaten einführen, das einfachste Automatenmodell, das aber recht nützlich ist und als Grundlage für weitere Automatenmodell dient.
Gehen wir nun davon aus, dass der Lichtschalter zu Beginn ausgeschaltet ist, so soll der Zustand 'aus' zudem der (eindeutige) Startzustand sein. Wollen wir ferner bspw. ein System modellieren, in dem nur jene Aktionsfolgen „gut“ sind, bei denen das Licht am Ende wieder ausgeschaltet ist, so modellieren wir den Zustand 'aus' noch als Endzustand. Abbildung 2.2 zeigt das ergänzte System. Der Pfeil in den Zustand 'aus' hinein deutet an, dass 'aus' der Startzustand ist. Der doppelte Kreis um 'aus' bedeutet, dass 'aus' ein Endzustand ist.
Damit haben wir bereits alle Komponenten eines endlichen Automaten vorliegen.
Wichtig ist bei diesem Beispiel, dass
- wir ein System mit einer endlichen Anzahl von Zuständen haben,
- von denen einer als Startzustand und
- eine beliebige Teilmenge als Endzustände hervorgehoben sind,
- dass Zustandsübergänge möglich sind und
- dass das System sich stets in genau einem Zustand befindet.
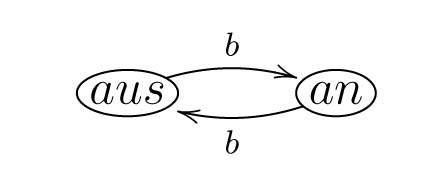
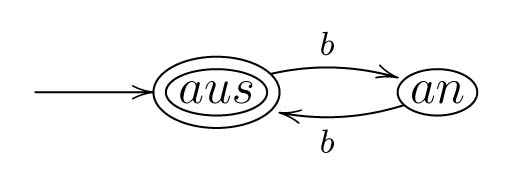
Das dynamische Verhalten des Systems lässt sich wie folgt beschreiben: Wir beginnen im Startzustand (hier 'aus'). Dann können genau die Aktionen ausgeführt werden, die mit Kanten aus diesem Zustand herausgehen. In diesem Fall gibt es nur die Aktion \(b\), die uns in den Zustand 'an' überführt. Von dort geht es dann weiter. Führen wir die Aktion \(b\) bspw. dreimal hintereinander aus (wir schreiben dafür später \(b \cdot b \cdot b\) oder auch einfach \(bbb\)), so enden wir im Zustand 'an'. Führen wir \(b\) hingegen nur zweimal aus (also \(b \cdot b\)), so enden wir im Zustand 'aus'. Da 'aus' ein Endzustand ist, sagen wir, dass \(b \cdot b\) akzeptiert wird (\(bbb\) hingegen nicht, da 'an' kein Endzustand ist).

Das Eingabeband ist über dem Automaten notiert. Das Eingabewort ist \(abba\) (die weiteren leeren Kästchen und die schwarzen Punkte sollen andeuten, dass man auch längere Worte auf diesem Band notieren kann) und der gestrichelte Pfeil zwischen Automat und Eingabeband zeigt an, welcher Buchstabe des Wortes gerade gelesen wird (man spricht hier auch vom Lesekopf). Ist der Automat zu Anfang in \(z_0\), so kann er nun das \(a\) lesen (da es eine \(a\)-Kante aus \(z_0\) heraus gibt). Der Automat wechselt dann in den Zustand \(z_1\) und der Lesekopf wandert ein Feld weiter. Nun können die zwei \(b\) gelesen werden, wobei der Automat im Zustand \(z_1\) bleibt. Der letzte Buchstabe (das \(a\)) kann dann auch gelesen werden, wobei der Automat in den Zustand \(z_2\) wechselt. Da dies ein Endzustand ist und das Wort bis zum Ende gelesen wurde, akzeptiert der Automat das Wort \(abba\).
Die Vorstellung eines Eingabebandes ist historisch gewachsen und erscheint heute eher altertümlich. Sie ist aber eine gute Abstraktion und man kann sich recht gut überlegen, dass die Vorstellungen eines Wortes im (Haupt-)Speicher oder einer Folge von Aktionen wie zu Anfang recht ähnlich sind. Das wichtige ist hier der Automat, der ein Wort von links nach rechts liest und dieses letztendlich akzeptiert oder nicht. Nicht akzeptiert wird dabei ein Wort dann, wenn entweder das Wort gar nicht zu Ende gelesen werden kann (dies tritt auf, wenn der Automat in einem Zustand \(z\) ist und einen Buchstaben \(x\) lesen soll, zu dem es keine Kante aus \(z\) heraus gibt; man sagt dann, der Automat blockiert) oder aber das Wort zu Ende gelesen werden kann, der Automat dann aber nicht in einem Endzustand ist.
Die Menge aller Wörter, die ein gegebener Automat akzeptiert, bezeichnen wir als seine akzeptierte Sprache. Warum diese wichtig ist, werden wir in der Vorlesung genauer behandeln. Im obigen Beispiel aus Abbildung 2.2 akzeptieren wir z.B. genau die Wörter, die nur aus \(b\)s bestehen und die eine gerade Anzahl \(b\)s enthalten. Im Beispiel aus Abbidlung 2.3 werden jene Wörter aus \(a\)s und \(b\)s akzeptiert, die mit genau einem \(a\) beginnen und enden und die dazwischen beliebig viele (auch \(0\)) \(b\)s haben.
Man kann sich die Frage stellen, ob solche Automaten einen Anwendungsfall haben, da sie recht einfach erscheinen. Erstens sind solche endlichen Automaten die Grundlage für prinzipiell alle weiteren Automatenmodelle, mit denen dann sehr viel komplexere Systeme modelliert werden können. Zweitens sind bereits endliche Automaten für viele Anwendungen von Bedeutung. Bspw. basiert die Worterkennung bei einem Compiler (um bspw. das Schlüsselwort 'if' zu finden) auf endlichen Automaten. Auch Protokolle und viele Anwendungen aus der technischen Informatik lassen sich mit endlichen Automaten (oder leichten Varianten davon) modellieren und dann implementieren (nachdem sich das Modell als hoffentlich fehlerfrei erwiesen hat).
