Statt Formeln als Zeichenketten der Art \((A \wedge B)\) auszudrücken, kann man Formeln auch als Bäume, sogenannte Strukturbäume, ausdrücken. Dies ist für manche Algorithmen hilfreich.

Ein Strukturbaum zu einer Formel \(F\) ist ein Baum, bei dem die inneren Knoten (die Knoten, die keine Blätter sind) Junktoren sind und die Blätter die atomaren (Teil-)Formeln von \(F\).

Im einzelnen:

1. Der Hauptoperator markiert die Wurzel.
2. Teilformeln entsprechen Teilbäumen.
3. Die Reihenfolge der Teilformeln wird beibehalten (linke Teilformel, linkes Kind).
4. Die Aussagesymbole werden dann die Blätter des Baumes.
5. Die Junktoren sind die inneren Knoten. Dabei hat \(\neg\) ein Kind, alle anderen Junktoren haben zwei Kinder.

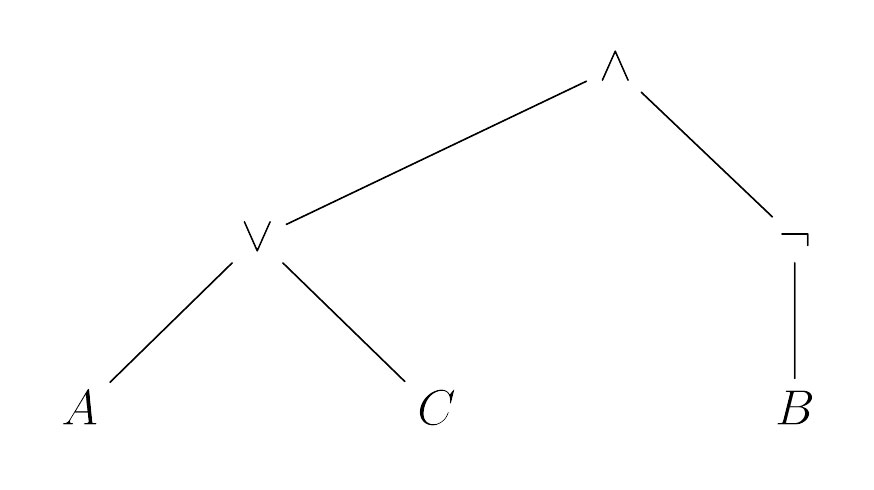
Ein Beispiel veranschaulicht dies schnell. Sei \(F = ((A \vee C) \wedge \neg B)\), dann ergibt sich als Strukturbaum zu \(F\)